NCERT Solutions for Class 11 Maths Chapter 2
Posted inStudy Material

NCERT Solutions for Class 11 Maths Chapter 2

Download PDF πŸ“„

NCERT Solutions for Class 11 Maths Chapter 2, Relations and Functions, are thorough in teaching the students some of the fundamental concepts associated with the topic. This concept introduces students to the central idea of relations, such as connections between elements of two sets, and functions – a special type of relation where every element in the domain corresponds to exactly one element in the range. The chapter covers key topics such as types of relations (reflexive, symmetric, transitive, and equivalence relations), domain, co-domain, and range of a function, and various operations on sets. It helps students build a strong foundation in understanding how relations and functions form the basis for more advanced mathematical concepts in calculus, algebra, and other branches of mathematics.

This will be very helpful for students so that they may practice a range of different problems in their master examinations. NCERT Solutions exercises at the end test various levels of difficulties with the proper understanding and application of those concepts in a problem to solve it. This can help students understand the relations and functions better with solutions like these and become confident in solving such questions. This chapter also covers the application of functions and relations to real life, making such abstract mathematical concepts more related and understandable.

Exercise 2.1

  1. If find the values of x and y.

Certainly, let’s solve the equation:

Given:

(x/3 + 1, y – 2/3) = (5/3, 1/3)

Solution:

For two ordered pairs to be equal, their corresponding components must be equal. Therefore, we can set up the following system of equations:

x/3 + 1 = 5/3

y – 2/3 = 1/3

Solving for x:

x/3 + 1 = 5/3

x/3 = 5/3 – 1

x/3 = 2/3

x = 2

Solving for y:

y – 2/3 = 1/3

y = 1/3 + 2/3

y = 1

Therefore, the values of x and y are:

x = 2

y = 1

  1. If set A has 3 elements and set B = {3, 4, 5}, then find the number of elements in (A Γ— B).

Certainly, let’s find the number of elements in (A x B).

Given:

  • Set A has 3 elements.
  • Set B = {3, 4, 5}

Solution:

The Cartesian product (A x B) is the set of all possible ordered pairs where the first element is from set A and the second element is from set B.

Since set A has 3 elements and set B has 3 elements, the number of elements in (A x B) will be the product of their cardinalities (number of elements).

Therefore, the number of elements in (A x B) is 3 x 3 = 9.

  1. If G = {7, 8} and H = {5, 4, 2}, find G Γ— H and H Γ— G.

Solution:

G Γ— H:

We pair each element of G with each element of H to form ordered pairs:

G Γ— H = {(7,5), (7,4), (7,2), (8,5), (8,4), (8,2)}

H Γ— G:

Similarly, we pair each element of H with each element of G:

H Γ— G = {(5,7), (5,8), (4,7), (4,8), (2,7), (2,8)}

As you can see, G Γ— H and H Γ— G are different sets, even though they have the same number of elements. The order of the elements in the ordered pairs matters.

  1. State whether each of the following statements is true or false. If the statement is false, rewrite the given statement correctly.

(i) If P = {m, n} and Q = {n, m}, then P Γ— Q = {(m, n), (n, m)}

(ii) If A and B are non-empty sets, then A Γ— B is a non-empty set of ordered pairs (x, y) such that x ∈ A and y ∈ B.

(iii) If A = {1, 2}, B = {3, 4}, then A Γ— (B ∩ Ξ¦) = Ξ¦

Solution:

(i) False. The correct statement is: P Γ— Q = {(m, n), (m, m), (n, n), (n, m)}. We pair each element of P with each element of Q to form ordered pairs.

(ii) True. This is the definition of the Cartesian product of two sets.

(iii) True. The intersection of any set with the empty set is the empty set. Therefore, B ∩ Ξ¦ = Ξ¦. So, A Γ— (B ∩ Ξ¦) = A Γ— Ξ¦ = Ξ¦.

  1. If A = {–1, 1}, find A Γ— A Γ— A.

To find A Γ— A Γ— A, we need to pair each element of A with every other element of A, including itself, three times.

Here are the possible combinations:

A Γ— A Γ— A = { (-1, -1, -1), (-1, -1, 1), (-1, 1, -1), (-1, 1, 1),

    (1, -1, -1), (1, -1, 1), (1, 1, -1), (1, 1, 1)}

So, A Γ— A Γ— A contains 8 elements.

  1. If A Γ— B = {(a, x), (a, y), (b, x), (b, y)}. Find A and B.

From the given Cartesian product A Γ— B, we can observe the following:

  • The first elements of the ordered pairs are ‘a’ and ‘b’. So, A = {a, b}.
  • The second elements of the ordered pairs are ‘x’ and ‘y’. So, B = {x, y}.

Therefore, A = {a, b} and B = {x, y}.

  1. Let A = {1, 2}, B = {1, 2, 3, 4}, C = {5, 6} and D = {5, 6, 7, 8}. Verify that

(i) A Γ— (B ∩ C) = (A Γ— B) ∩ (A Γ— C)

(ii) A Γ— C is a subset of B Γ— D

Solution:

Part (i):

Step 1: Calculate B ∩ C

B ∩ C = {1, 2, 3, 4} ∩ {5, 6} = {} (empty set)

Step 2: Calculate A Γ— (B ∩ C)

A Γ— (B ∩ C) = A Γ— {} = {} (empty set)

Step 3: Calculate A Γ— B and A Γ— C

A Γ— B = {(1, 1), (1, 2), (1, 3), (1, 4), (2, 1), (2, 2), (2, 3), (2, 4)} A Γ— C = {(1, 5), (1, 6), (2, 5), (2, 6)}

Step 4: Calculate (A Γ— B) ∩ (A Γ— C)

(A Γ— B) ∩ (A Γ— C) = {} (empty set)

Conclusion for Part (i):

Since A Γ— (B ∩ C) = {} and (A Γ— B) ∩ (A Γ— C) = {}, the equation A Γ— (B ∩ C) = (A Γ— B) ∩ (A Γ— C) is verified.

Part (ii):

Step 1: Calculate A Γ— C

A Γ— C = {(1, 5), (1, 6), (2, 5), (2, 6)}

Step 2: Calculate B Γ— D

B Γ— D = {(1, 5), (1, 6), (1, 7), (1, 8), (2, 5), (2, 6), (2, 7), (2, 8), (3, 5), (3, 6), (3, 7), (3, 8), (4, 5), (4, 6), (4, 7), (4, 8)}

Conclusion for Part (ii): Every element of A Γ— C is also an element of B Γ— D. Therefore, A Γ— C is a subset of B Γ— D.

  1. Let A = {1, 2} and B = {3, 4}. Write A Γ— B. How many subsets will A Γ— B have? List them.

Solution:

A Γ— B = {(1,3), (1,4), (2,3), (2,4)}

Since A Γ— B has 4 elements, it will have 2^4 = 16 subsets.

Here are the 16 subsets:

Empty set: {}

Single-element subsets: {(1,3)}, {(1,4)}, {(2,3)}, {(2,4)}

Two-element subsets:

  • {(1,3), (1,4)}
  • {(1,3), (2,3)}
  • {(1,3), (2,4)}
  • {(1,4), (2,3)}
  • {(1,4), (2,4)}
  • {(2,3), (2,4)}

Three-element subsets:

  • {(1,3), (1,4), (2,3)}
  • {(1,3), (1,4), (2,4)}
  • {(1,3), (2,3), (2,4)}
  • {(1,4), (2,3), (2,4)}

Four-element subset (the entire set): {(1,3), (1,4), (2,3), (2,4)}

  1.  Let A and B be two sets such that n(A) = 3 and n (B) = 2. If (x, 1), (y, 2), (z, 1) are in A Γ— B, find A and B, where x, y and z are distinct elements.

Solution:

We know that A Γ— B = {(x, 1), (y, 2), (z, 1)}.

Finding Set B:

From the ordered pairs, we can see that the second elements are 1 and 2. Therefore, B = {1, 2}.

Finding Set A:

The first elements of the ordered pairs are x, y, and z. Since n(A) = 3, we can conclude that A = {x, y, z}.

Therefore, A = {x, y, z} and B = {1, 2}.

  1. The Cartesian product A Γ— A has 9 elements among which are found (–1, 0) and (0, 1). Find the set A and the remaining elements of A Γ— A.

The Cartesian product A Γ— A has 9 elements among which are found (–1, 0) and (0, 1). Find the set A and the remaining elements of A Γ— A.

Solution:

We know that the Cartesian product of a set A with itself, A Γ— A, is the set of all ordered pairs (a, b) where a and b are elements of A.
We are given that |A Γ— A| = 9. This means that the cardinality (number of elements) of A is 3, since 3 * 3 = 9.
From the two given elements (-1, 0) and (0, 1), we can deduce that -1, 0, and 1 are elements of A.
Therefore, A = {-1, 0, 1}.
Now, we can calculate the remaining elements of A Γ— A: 

A Γ— A = {(-1, -1), (-1, 0), (-1, 1), (0, -1), (0, 0), (0, 1), (1, -1), (1, 0), (1, 1)}

So, the remaining elements of A Γ— A are: (-1, -1), (-1, 1), (0, -1), (0, 0), (1, -1), (1, 0), and (1, 1).

Download NCERT Solutions for Class 11 Maths Chapter 2 PDF

Exercise 2.2

  1. Let A = {1, 2, 3, … , 14}. Define a relation R from A to A by R = {(x, y): 3x – y = 0, where x, y ∈ A}. Write down its domain, codomain and range.

Solution: 

Let’s analyze the given relation R:

R = {(x, y): 3x – y = 0, where x, y ∈ A}

This relation can be rewritten as:

R = {(x, y): y = 3x, where x, y ∈ A}

Now, let’s find the domain, codomain, and range:

Domain:

The domain of R is the set of all first elements of the ordered pairs in R.

From the equation y = 3x, we can see that for each x in A, there is a corresponding y in A. However, not all x in A will yield a y in A.

To find the valid x values, we need to ensure that 3x ≀ 14 (since the maximum value in A is 14). This gives us:

x ≀ 14/3 β‰ˆ 4.67

Therefore, the domain of R is the set of integers less than or equal to 4.67, which are:

Domain = {1, 2, 3, 4}

Codomain:

The codomain of R is the set A itself, as the relation is defined from A to A.

Codomain = {1, 2, 3, …, 14}

Range:

The range of R is the set of all second elements of the ordered pairs in R.

From the equation y = 3x, we can see that the possible values of y are multiples of 3 that are less than or equal to 14.

Therefore, the range of R is:

Range = {3, 6, 9, 12}

  1. Define a relation R on the set N of natural numbers by R = {(x, y): y = x + 5, x is a natural number less than 4; x, y ∈ N}. Depict this relationship using roster form. Write down the domain and the range.

Solution:

Given relation R: {(x, y): y = x + 5, x is a natural number less than 4; x, y ∈ N}

Since x is a natural number less than 4, the possible values of x are 1, 2, and 3.

For each value of x, we can calculate the corresponding y:

  • For x = 1, y = 1 + 5 = 6
  • For x = 2, y = 2 + 5 = 7
  • For x = 3, y = 3 + 5 = 8

Therefore, the relation R in roster form is:

R = {(1, 6), (2, 7), (3, 8)}

Domain:

The domain of R is the set of all first elements of the ordered pairs in R.

Domain = {1, 2, 3}

Range:

The range of R is the set of all second elements of the ordered pairs in R.

Range = {6, 7, 8}

  1. A = {1, 2, 3, 5} and B = {4, 6, 9}. Define a relation R from A to B by R = {(x, y): the difference between x and y is odd; x ∈ A, y ∈ B}. Write R in roster form.

Given:

* A = {1, 2, 3, 5}

* B = {4, 6, 9}

* Relation R: {(x, y): the difference between x and y is odd; x ∈ A, y ∈ B}

We need to find all pairs (x, y) where x is from A, y is from B, and their difference is odd.

Let’s check each combination:

1. For x = 1:

   y = 4: |1 – 4| = 3 (odd) – Include (1, 4)

   y = 6: |1 – 6| = 5 (odd) – Include (1, 6)

   y = 9: |1 – 9| = 8 (even) – Exclude

2. For x = 2:

   y = 4: |2 – 4| = 2 (even) – Exclude

   y = 6: |2 – 6| = 4 (even) – Exclude

   y = 9: |2 – 9| = 7 (odd) – Include (2, 9)

3. For x = 3:

   y = 4: |3 – 4| = 1 (odd) – Include (3, 4)

   y = 6: |3 – 6| = 3 (odd) – Include (3, 6)

   y = 9: |3 – 9| = 6 (even) – Exclude

4. For x = 5:

   y = 4: |5 – 4| = 1 (odd) – Include (5, 4)

   y = 6: |5 – 6| = 1 (odd) – Include (5, 6)

   y = 9: |5 – 9| = 4 (even) – Exclude

Therefore, the relation R in roster form is:

R = {(1, 4), (1, 6), (2, 9), (3, 4), (3, 6), (5, 4), (5, 6)}

  1. The figure shows a relationship between the sets P and Q. Write this relation

(i) in set-builder form (ii) in roster form

What is its domain and range?

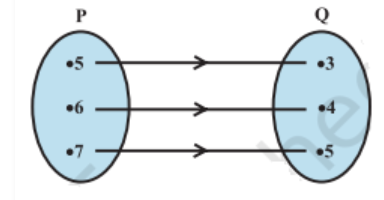
Solution:

i) Set-builder form:

The relation R can be defined as:

R = {(x, y) | x ∈ P, y ∈ Q, and (x, y) is an arrow from P to Q}

ii) Roster form:

From the diagram, we can see the following pairs:

R = {(5, 3), (5, 4), (5, 5), (6, 3), (6, 4), (6, 5), (7, 3), (7, 4), (7, 5)}

Domain:

The domain of R is the set of all first elements of the ordered pairs in R.

Domain = {5, 6, 7}

Range:

The range of R is the set of all second elements of the ordered pairs in R.

Range = {3, 4, 5}

  1.  Let A = {1, 2, 3, 4, 6}. Let R be the relation on A defined by

{(a, b): a, b ∈ A, b is exactly divisible by a}.

(i) Write R in roster form

(ii) Find the domain of R

(iii) Find the range of R

Solution:

i) Roster form of R:

We need to find all pairs (a, b) where a and b are from A and b is exactly divisible by a.

Let’s check each combination:

  • For a = 1: All elements in A are divisible by 1. So, pairs are: (1, 1), (1, 2), (1, 3), (1, 4), (1, 6)
  • For a = 2: Only 2, 4, and 6 are divisible by 2. So, pairs are: (2, 2), (2, 4), (2, 6)
  • For a = 3: Only 3 and 6 are divisible by 3. So, pairs are: (3, 3), (3, 6)
  • For a = 4: Only 4 is divisible by 4. So, the pair is: (4, 4)
  • For a = 6: Only 6 is divisible by 6. So, the pair is: (6, 6)

Therefore, the relation R in roster form is:

R = {(1, 1), (1, 2), (1, 3), (1, 4), (1, 6), (2, 2), (2, 4), (2, 6), (3, 3), (3, 6), (4, 4), (6, 6)}

ii) Domain of R:

The domain of R is the set of all first elements of the ordered pairs in R.

Domain = {1, 2, 3, 4, 6}

iii) Range of R:

The range of R is the set of all second elements of the ordered pairs in R.

Range = {1, 2, 3, 4, 6}

  1. Determine the domain and range of the relation R defined by R = {(x, x + 5): x ∈ {0, 1, 2, 3, 4, 5}}.

The relation R is defined as:

R = {(x, x + 5): x ∈ {0, 1, 2, 3, 4, 5}}

This means that for each x in the set {0, 1, 2, 3, 4, 5}, we form an ordered pair (x, x + 5).

Domain:

The domain of R is the set of all first elements of the ordered pairs in R.

In this case, the first elements are the values of x. So, the domain is:

Domain = {0, 1, 2, 3, 4, 5}

Range:

The range of R is the set of all second elements of the ordered pairs in R.

To find the second elements, we add 5 to each x value in the domain:

  • For x = 0, x + 5 = 5
  • For x = 1, x + 5 = 6
  • For x = 2, x + 5 = 7
  • For x = 3, x + 5 = 8
  • For x = 4, x + 5 = 9
  • For x = 5, x + 5 = 10

So, the range is:

Range = {5, 6, 7, 8, 9, 10}

  1. Write the relation R = {(x, x3): x is a prime number less than 10} in roster form.

The prime numbers less than 10 are 2, 3, 5, and 7.

Therefore, the relation R in roster form is:

R = {(2, 8), (3, 27), (5, 125), (7, 343)}

  1. To find the number of relations from A to B, we need to consider the Cartesian product A Γ— B.

To find the number of relations from A to B, we need to consider the Cartesian product A Γ— B.

A Γ— B = {(x, 1), (x, 2), (y, 1), (y, 2), (z, 1), (z, 2)}

Each element in A Γ— B can either be included or excluded from a relation. So, for each element, we have 2 choices.

Since there are 6 elements in A Γ— B, the total number of possible combinations (i.e., the number of subsets of A Γ— B) is 26.

Therefore, the number of relations from A to B is 26.

  1.  Let R be the relation on Z defined by R = {(a, b): a, b ∈ Z, a – b is an integer}. Find the domain and range of R.

The relation R is defined as:

R = {(a, b): a, b ∈ Z, a – b is an integer}

Domain:

The domain of R is the set of all first elements of the ordered pairs in R.

Since a – b is an integer for any integers a and b, every integer can be the first element of an ordered pair in R.

Therefore, the domain of R is the set of all integers, Z.

Range:

The range of R is the set of all second elements of the ordered pairs in R.

Similarly, any integer b can be the second element of an ordered pair in R, as we can always find an integer a such that a – b is an integer.

Therefore, the range of R is also the set of all integers, Z.

Exercise 2.3

  1. Which of the following relations are functions? Give reasons. If it is a function, determine its domain and range.

(i) {(2, 1), (5, 1), (8, 1), (11, 1), (14, 1), (17, 1)}

(ii) {(2, 1), (4, 2), (6, 3), (8, 4), (10, 5), (12, 6), (14, 7)}

(iii) {(1, 3), (1, 5), (2, 5)}

Solution:

A relation is a function if each input (x-value) corresponds to exactly one output (y-value).

Let’s analyze each relation:

i) {(2, 1), (5, 1), (8, 1), (11, 1), (14, 1), (17, 1)}

  • Each input (x-value) has exactly one output (y-value).
  • This relation is a function.
  • Domain: {2, 5, 8, 11, 14, 17}
  • Range: {1}

ii) {(2, 1), (4, 2), (6, 3), (8, 4), (10, 5), (12, 6), (14, 7)}

  • Each input (x-value) has exactly one output (y-value).
  • This relation is a function.
  • Domain: {2, 4, 6, 8, 10, 12, 14}
  • Range: {1, 2, 3, 4, 5, 6, 7}

iii) {(1, 3), (1, 5), (2, 5)}

  • The input 1 corresponds to two different outputs, 3 and 5.
  • This relation is not a function.
  1. Find the domain and range of the following real function:

(i) f(x) = –|x| (ii) f(x) = √(9 – x2) 

Solution:

i) f(x) = -|x|

  • Domain: The absolute value function |x| is defined for all real numbers. Therefore, the domain of f(x) = -|x| is also all real numbers.
    Domain: (-∞, ∞)
  • Range: The absolute value function |x| always gives a non-negative value. So, -|x| will always be non-positive.
    Range: (-∞, 0]

ii) f(x) = √(9 – xΒ²)

  • Domain: For the square root to be defined, the expression inside must be non-negative:
    9 – xΒ² β‰₯ 0 xΒ² ≀ 9 -3 ≀ x ≀ 3
    Domain: [-3, 3]
  • Range: The maximum value of √(9 – xΒ²) occurs when x = 0, which is √9 = 3. The minimum value is 0, which occurs at the endpoints of the domain, x = -3 and x = 3.
    Range: [0, 3]
  1. A function f is defined by f(x) = 2x – 5. Write down the values of

(i) f(0), (ii) f(7), (iii) f(–3)

To find the values of f(0), f(7), and f(-3), we simply substitute the values of x into the function f(x) = 2x – 5.

i) f(0): f(0) = 2(0) – 5 = 0 – 5 = -5

ii) f(7): f(7) = 2(7) – 5 = 14 – 5 = 9

iii) f(-3): f(-3) = 2(-3) – 5 = -6 – 5 = -11

Therefore:

  • f(0) = -5
  • f(7) = 9
  • f(-3) = -11
  1.  The function β€˜t’, which maps temperature in degree Celsius into temperature in degree Fahrenheit is defined by

Solution:

NCERT Solutions for Class 11 Maths Chapter 2
  1. Find the range of each of the following functions:

(i) f(x) = 2 – 3x, x ∈ R, x > 0

(ii) f(x) = x2 + 2, x is a real number

(iii) f(x) = x, x is a real number

Solution:

Let’s analyze each function and find its range.

(i) f(x)=2βˆ’3xf(x) = 2 – 3x, where x∈Rx \in \mathbb{R} and x>0x > 0

NCERT Solutions for Class 11 Maths Chapter 2

Miscellaneous Exercise

  1. The relation f is defined by {f(x)= x2, 0≀x≀3 3x, 3≀x≀10}

The relation g is defined by {g(x)=x2, 0≀x≀2 3x, 2≀x≀10}

Show that f is a function and g is not a function.

Let’s analyze the relations f and g to determine if they are functions.

Relation f:

f(x) = {x^2, 0 ≀ x ≀ 3 {3x, 3 ≀ x ≀ 10

Relation g:

g(x) = {x^2, 0 ≀ x ≀ 2 {3x, 2 ≀ x ≀ 10

Understanding Functions:

A relation is considered a function if each input (x-value) corresponds to exactly one output (y-value). In other words, for every x-value, there should be only one1 associated y-value.

Analyzing Relation f:

  • For 0 ≀ x < 3, f(x) = x^2. This part of the function is well-defined and each input has a unique output.
  • For 3 < x ≀ 10, f(x) = 3x. Again, this part is well-defined and each input has a unique output.
  • At the boundary point x = 3, both definitions give the same value: f(3) = 3^2 = 9 and f(3) = 3 * 3 = 9.

Therefore, for all x in the domain [0, 10], f(x) has a unique output. Hence, f is a function.

Analyzing Relation g:

  • For 0 ≀ x < 2, g(x) = x^2. This part is well-defined.
  • For 2 < x ≀ 10, g(x) = 3x. This part is also well-defined.
  • However, at the boundary point x = 2, we have:
    • g(2) = 2^2 = 4 (from the first part)
    • g(2) = 3 * 2 = 6 (from the second part)

This means that for the input x = 2, we have two different outputs (4 and 6). This violates the definition of a function.

Therefore, g is not a function.

In conclusion:

  • Relation f is a function because each input has a unique output.
  • Relation g is not a function because the input 2 has multiple outputs.
  1. If f(x) = x2, find

Let’s break down the given expression:

f(1.1) – f(1) / (1.1 – 1)

Step 1: Calculate f(1.1)

Since f(x) = xΒ², we can substitute x with 1.1:

f(1.1) = (1.1)Β² = 1.21

Step 2: Calculate f(1)

Similarly, substituting x with 1:

f(1) = (1)Β² = 1

Step 3: Substitute the values into the expression

Now, we can replace f(1.1) and f(1) in the original expression:

(1.21 – 1) / (1.1 – 1)

Step 4: Simplify the expression

0.21 / 0.1 = 2.1

Therefore, the value of the expression is 2.1

  1. Find the domain of the function

To find the domain of the function f(x) = (x^2 + 2x + 1) / (x^2 – 8x + 12), we need to identify the values of x that would make the denominator zero. This is because division by zero is undefined.

So, we need to solve the equation:

x^2 – 8x + 12 = 0

Factoring this quadratic equation, we get:

(x – 2)(x – 6) = 0

This equation is satisfied when x = 2 or x = 6.

Therefore, the function is undefined at x = 2 and x = 6.

Hence, the domain of the function f(x) is all real numbers except 2 and 6.

In interval notation, the domain can be expressed as:

Domain: (-∞, 2) U (2, 6) U (6, ∞)

  1. Find the domain and the range of the real function f defined by f(x) = √(x – 1).

Domain:

For the square root to be defined, the expression inside must be non-negative:

x – 1 β‰₯ 0 x β‰₯ 1

Therefore, the domain of f(x) is [1, ∞).

Range:

The square root function always gives a non-negative value. So, the minimum value of √(x-1) is 0, which occurs when x = 1. As x increases beyond 1, √(x-1) also increases without bound.

Therefore, the range of f(x) is [0, ∞).

  1. Find the domain and the range of the real function f defined by f (x) = |x – 1|.

Let’s analyze the function f(x)=∣xβˆ’1∣f(x) = |x – 1|, which involves the absolute value of the expression xβˆ’1x – 1.

Domain of f(x)=∣xβˆ’1∣f(x) = |x – 1|:

The domain of a function refers to the set of all possible values of xx for which the function is defined. The absolute value function ∣xβˆ’1∣|x – 1| is defined for all real numbers xx, because we can always calculate the absolute value of any real number.

Thus, the domain of f(x)=∣xβˆ’1∣f(x) = |x – 1| is:

Domain of f(x)=R(all real numbers).\text{Domain of } f(x) = \mathbb{R} \quad \text{(all real numbers)}.

Range of f(x)=∣xβˆ’1∣f(x) = |x – 1|:

The range of a function refers to the set of all possible output values of f(x)f(x) when xx varies over the domain.

  • The absolute value function ∣xβˆ’1∣|x – 1| always gives a non-negative result because the absolute value of any real number is never negative.
  • The smallest value of ∣xβˆ’1∣|x – 1| occurs when x=1x = 1, as ∣1βˆ’1∣=0|1 – 1| = 0.
  • As xx moves further from 1 (either to the left or right), the value of ∣xβˆ’1∣|x – 1| increases without bound.

Therefore, the range of f(x)=∣xβˆ’1∣f(x) = |x – 1| is all non-negative real numbers, i.e.,

Range of f(x)=[0,∞).\text{Range of } f(x) = [0, \infty).

Final Answer:

  • Domain: R\mathbb{R} (all real numbers).
  • Range: [0,∞)[0, \infty) (non-negative real numbers).
  1.  Let be a function from R into R. Determine the range of f.

The function f is defined as:

f = {(x, x2 / (1 + x2)): x ∈ R}

This means that for every real number x, f maps x to x2 / (1 + x2).

To find the range of f, we need to determine all possible values of f(x) as x varies over all real numbers.

Let’s analyze the expression x2 / (1 +x2):

  • The denominator, 1 + x2, is always positive for any real value of x.
  • The numerator, x2, is also always non-negative.
  • Therefore, the fraction x2 / (1 + x2) is always non-negative.

As x approaches positive or negative infinity, the fraction approaches 1. This is because the denominator grows much faster than the numerator.

So, the range of f is the set of all non-negative real numbers less than or equal to 1.

Range of f = [0, 1)

  1. Let f, g: R β†’ R be defined, respectively by f(x) = x + 1, g(x) = 2x – 3. Find f + g, f – g and f/g.

To find f + g, f – g, and f/g, we simply perform the indicated operations on the functions f(x) and g(x).

f + g:

(f + g)(x) = f(x) + g(x) = (x + 1) + (2x – 3) = 3x – 2

f – g:

(f – g)(x) = f(x) – g(x) = (x + 1) – (2x – 3) = -x + 4

f / g:

(f / g)(x) = f(x) / g(x) = (x + 1) / (2x – 3)

However, we need to consider the domain of f/g. The denominator cannot be zero, so 2x – 3 β‰  0. This means x β‰  3/2.

Therefore, the domain of f/g is all real numbers except 3/2.

In summary:

  • (f + g)(x) = 3x – 2
  • (f – g)(x) = -x + 4
  • (f / g)(x) = (x + 1) / (2x – 3), x β‰  3/2
  1. Let f = {(1, 1), (2, 3), (0, –1), (–1, –3)} be a function from Z to Z defined by f(x) = ax + b, for some integers a, b. Determine a, b.

We are given the function f(x) = ax + b and some of its values:

  • f(1) = 1
  • f(2) = 3
  • f(0) = -1
  • f(-1) = -3

We can use these values to create a system of equations:

  1. a(1) + b = 1
  2. a(2) + b = 3
  3. a(0) + b = -1
  4. a(-1) + b = -3

From equation 3, we can directly see that b = -1.

Substituting b = -1 in equation 1, we get: a – 1 = 1 a = 2

Therefore, the values of a and b are: a = 2 b = -1

So, the function f(x) is defined as: f(x) = 2x – 1

9. Let R be a relation from N to N defined by R = {(a, b): a, b ∈ N and a = b2}. Are the following true?

(i) (a, a) ∈ R, for all a ∈ N
(ii) (a, b) ∈ R, implies (b, a) ∈ R

(iii) (a, b) ∈ R, (b, c) ∈ R implies (a, c) ∈ R

Justify your answer in each case.

Solution:

(i) False: For (a, a) to be in R, we must have a = aΒ². This is only true for a = 1. For any other natural number, a β‰  aΒ². Therefore, (a, a) is not in R for all a ∈ N.

(ii) False: Let’s consider an example: (9, 3) ∈ R because 9 = 3Β². However, (3, 9) βˆ‰ R because 3 β‰  9Β². This counterexample shows that the statement is not true in general.

(iii) False: Consider the following: (9, 3) ∈ R and (16, 4) ∈ R. However, (9, 4) βˆ‰ R because 9 β‰  4Β². This shows that even if (a, b) ∈ R and (b, c) ∈ R, it does not necessarily imply that (a, c) ∈ R.

10. Let A = {1, 2, 3, 4}, B = {1, 5, 9, 11, 15, 16} and f = {(1, 5), (2, 9), (3, 1), (4, 5), (2, 11)}. Are the following true?

(i) f is a relation from A to B (ii) f is a function from A to B

Justify your answer in each case.

Solution:

(i) True: A relation from A to B is a subset of the Cartesian product A Γ— B. Here, f is a subset of A Γ— B, so it is a relation from A to B.

(ii) False: A function from A to B must assign exactly one element of B to each element of A. However, in f, the element 2 in A is assigned to both 9 and 11 in B. This violates the definition of a function.

11. Let f be the subset of Z Γ— Z defined by f = {(ab, a + b): a, b ∈ Z}. Is f a function from Z to Z: justify your answer.

No, f is not a function from Z to Z.

To be a function, each element in the domain (Z in this case) must be associated with exactly one element in the codomain (also Z). However, in this case, a single element in the domain can be associated with multiple elements in the codomain.

For example, consider the number 4 in the domain. It can be obtained by multiplying 1 and 4, or 2 and 2.

  • If a = 1 and b = 4, then ab = 4 and a + b = 5. So, (4, 5) ∈ f.
  • If a = 2 and b = 2, then ab = 4 and a + b = 4. So, (4, 4) ∈ f.

As you can see, the element 4 in the domain is associated with both 5 and 4 in the codomain. This violates the definition of a function.

Therefore, f is not a function from Z to Z.

12.  Let A = {9, 10, 11, 12, 13} and let f: A β†’ N be defined by f(n) = the highest prime factor of n. Find the range of f.

To find the range of f, we need to find the highest prime factor of each element in A and then collect those prime factors into a set.

  • f(9): The highest prime factor of 9 is 3.
  • f(10): The highest prime factor of 10 is 5.
  • f(11): The highest prime factor of 11 is 11 (since 11 is prime).
  • f(12): The highest prime factor of 12 is 3.
  • f(13): The highest prime factor of 13 is 13 (since 13 is prime).

Therefore, the range of f is the set {3, 5, 11, 13}.

NCERT Solutions for Class 11 Maths Chapter 2 FAQs

What are the key concepts covered in Chapter 2 of Class 11 Maths?

This chapter typically covers Sets, Relations, and Functions, including topics like types of sets, set operations, and the concept of functions.

How can I understand the different types of sets in Chapter 2?

The chapter explains various types of sets, such as finite, infinite, equal, null, singleton, and power sets. Practice examples and exercises in the NCERT solutions will help clarify these concepts.

What is the importance of relations and functions in Chapter 2?

Understanding relations and functions is crucial as they form the basis for many advanced topics in mathematics. The chapter explains their types and properties, helping students build a strong foundation for future learning.

Can I find step-by-step solutions for the exercises in Chapter 2?

Yes, the NCERT solutions provide detailed, step-by-step solutions to all the exercises in Chapter 2, making it easier for students to understand and apply the concepts.

How can I effectively practice the problems in Chapter 2?

To effectively practice, first read through the theoretical concepts carefully, then solve the exercises one by one. Reviewing the NCERT solutions will help you understand any mistakes and reinforce your learning.