Mathematics is a subject that takes up a major part of the Class 11 curriculum, as the foundation for advanced concepts in higher classes is built. Chapter 1 in the NCERT Class 11 Maths textbook is titled “Sets.” This is an introduction to the concept of a set, which is essential in understanding most of the subjects in mathematics. The topics covered include different types of sets, set notation, operations on sets, and fundamentals of Venn diagrams. A clear understanding of these basic concepts is essential for solving more complex problems in algebra, probability, and calculus. The NCERT solutions for this chapter provide detailed explanations, step-by-step procedures, and examples to help students grasp these concepts effectively.
The NCERT solutions for Class 11 Maths Chapter 1 are an invaluable resource for students, providing comprehensive guidance to solve exercise problems. These solutions cover all the important questions in the chapter from the basic concepts to complex problems ensuring that students can approach each one with confidence. Following these solutions, students can learn how to apply set theory in various mathematical contexts and improve their problem-solving skills. Whether it be exams or a better understanding of concepts, the NCERT solution is made easy, clear, and structured so that learning becomes apt for further maths topics.
Exercise 1.1 (Chapter 1 Sets)
1. Which of the following are sets? Justify your answer.
(i) The collection of all months of a year beginning with the letter J.
(ii) The collection of ten most talented writers of India.
(iii) A team of eleven best-cricket batsmen of the world.
(iv) The collection of all boys in your class.
(v) The collection of all natural numbers less than 100.
(vi) A collection of novels written by the writer Munshi Prem Chand.
(vii) The collection of all even integers.
(viii) The collection of questions in this Chapter.
(ix) A collection of most dangerous animals of the world.
Solution:
(i) The collection of all months of a year beginning with the letter J.
- Months starting with J: January, June, July
- Explanation: This collection is well-defined because the months that start with the letter “J” are clear and distinct. There is no ambiguity, and the collection has specific, identifiable elements.
- Therefore, This is a set.
(ii) The collection of ten most talented writers of India.
- Explanation: The term “most talented” is subjective and can vary depending on individual opinions, leading to ambiguity in defining who qualifies as one of the “most talented” writers. Since this collection is not clearly defined, we can’t precisely identify the members of this set.
- Therefore, This is not a set. The definition of “most talented” is vary person to person.
(iii) A team of eleven best cricket batsmen of the world.
- Explanation: The term “best” is subjective. Different people may have different opinions about who the best batsmen are. The collection is not clearly defined, as there is no universal agreement on who should be included.
- Therefore, This is not a set because it is not well-defined.
(iv) The collection of all boys in your class.
- Explanation: This collection is well-defined because it refers specifically to the boys in your class. There is no ambiguity regarding who is a member of the set, as they are clearly identifiable (the boys enrolled in the class).
- Therefore, This is a set.
(v) The collection of all natural numbers less than 100.
- Explanation: The set of natural numbers less than 100 is well-defined, and all the elements of the set are distinct. The numbers can be clearly listed as 1, 2, 3, …, 99.
- Therefore, This is a set.
(vi) A collection of novels written by the writer Munshi Prem Chand.
- Explanation: This collection is well-defined because it consists of a specific, identifiable group of objects: novels written by Munshi Prem Chand. These novels are distinct and identifiable.
- Therefore, This is a set.
(vii) The collection of all even integers.
- Explanation: The set of all even integers is well-defined, as even integers (numbers divisible by 2) are identified. The set includes numbers like 2, 4, 6, 8, and so on, extending infinitely.
- Therefore, This is a set.
(viii) The collection of questions in this Chapter.
- Explanation: This collection is well-defined because it refers specifically to the questions present in this chapter. There is no ambiguity regarding the elements of the set.
- Therefore, This is a set.
(ix) A collection of the most dangerous animals of the world.
- Explanation: The term “most dangerous” is subjective. Different people may have different opinions on which animals are the most dangerous, leading to an undefined collection.
- Therefore, This is not a set because it is not well-defined.
2. Let A = {1, 2, 3, 4, 5, 6}. Insert the appropriate symbol ∈or ∉ in the blank spaces:
(i) 5…A (ii) 8…A (iii) 0…A
(iv) 4…A (v) 2…A (vi) 10…A
Solution:
(i) 5∈A, 5 is present in the set A.
(ii) 8∉A, 8 is not present in the set A.
(iii) 0∉A, 0 is not present in the set A.
(iv) 4∈A, 4 is present in the set A.
(v) 2∈A, 2 is present in the set A.
(vi) 10∉A, 10 is not present in the set A.
3. Write the following sets in roster form:
(i) A = {x: x is an integer and –3 < x < 7}.
(ii) B = {x: x is a natural number less than 6}.
(iii) C = {x: x is a two-digit natural number such that the sum of its digits is 8}
(iv) D = {x: x is a prime number which is divisor of 60}.
(v) E = The set of all letters in the word TRIGONOMETRY.
(vi) F = The set of all letters in the word BETTER.
Solution:
(i) A={x:x is an integer and −3<x<7}
This set represents all integers between -3 and 7 (excluding -3 and 7). The integers in this range are: −2,−1,0,1,2,3,4,5,6
Roster form: A={−2,−1,0,1,2,3,4,5,6}
(ii) B={x:x is a natural number less than 6}
The natural numbers less than 6 are: 1, 2, 3, 4, 5.
Roster form: B={1,2,3,4,5}
(iii) C={x:x is a two-digit natural number such that the sum of its digits is 8}
We need to find two-digit natural numbers where the sum of their digits is 8. The possible numbers are: 17 (1 + 7 = 8), 26 (2 + 6 = 8), 35 (3 + 5 = 8), 44 (4 + 4 = 8), 53 (5 + 3 = 8), 62 (6 + 2 = 8), 71 (7 + 1 = 8), 80 (8 + 0 = 8).
Roster form: C={17,26,35,44,53,62,71,80}
(iv) D={x:x is a prime number which is a divisor of 60}
The prime numbers that divide 60 are 2, 3, and 5. These are the only prime divisors of 60.
Roster form: D={2,3,5}
(v) E=The set of all letters in the word TRIGONOMETRY
The unique letters in the word “TRIGONOMETRY” are T, R, I, G, O, N, M, E, and Y.
Roster form: E={T,R,I,G,O,N,M,E,Y}
(vi) F=The set of all letters in the word BETTER
The unique letters in the word “BETTER” are B, E, T, and R.
Roster form: F={B,E,T,R}
4. Write the following sets in the set-builder form:
(i) (3, 6, 9, 12)
(ii) {2, 4, 8, 16, 32}
(iii) {5, 25, 125, 625}
(iv) {2, 4, 6 …}
(v) {1, 4, 9 … 100}
Solutions:
(i) {3,6,9,12}
This set contains the first 4 multiples of 3. The elements of the set follow the pattern 3n, where n is a positive integer.
Set-builder form: {x:x=3n, n∈N, 1≤n≤4}
(Here, N represents the set of natural numbers, and n ranges from 1 to 4 for the given elements.)
(ii) {2,4,8,16,32}
This set contains powers of 2, specifically 21, 22, 23, 24, 25. The general form of these elements is 2n, where n is a positive integer.
Set-builder form: {x:x=2n, n∈N, 1≤n≤5}
(iii) {5,25,125,625}
This set contains powers of 5, specifically 51,52,53,54. The general form is 5n, where n is a positive integer.
Set-builder form: {x:x=5n, n∈N, 1≤n≤4}
(iv) {2,4,6,…}
This is the set of all even numbers. The general form of even numbers is 2n, where n is a positive integer.
Set-builder form: {x:x=2n, n∈N}
(v) {1,4,9,…,100}
This is the set of perfect squares (1, 4, 9, 16, …, 100). The general form for perfect squares is n2, where nnn is a positive integer, and nnn ranges from 1 to 10 for the given elements.
Set-builder form: {x:x=n2, n∈N, 1≤n≤10}
5. List all the elements of the following sets:
(i) A = {x: x is an odd natural number}
(ii) B = {x: x is an integer, -1/2 < x < 9/2}
(iii) C = {x: x is an integer, x2 ≤ 4}
(iv) D = {x: x is a letter in the word “LOYAL”}
(v) E = {x: x is a month of a year not having 31 days}
(vi) F = {x: x is a consonant in the English alphabet which proceeds k}.
Solution:
(i) A={x:x is an odd natural number}
The odd natural numbers are all the positive odd integers: 1, 3, 5, 7, 9, 11, 13, 15, 17, and so on.
List of elements: A={1,3,5,7,9,11,13,15,17,…}
(ii) B={x:x is an integer, −1/2<x<9/2}
The integers between −1/2 and 9/2 are 0, 1, 2, 3, 4.
List of elements: B={0,1,2,3,4}
(iii) C={x:x is an integer, x2≤4}
We need to find all integers such that their square is less than or equal to 4. The integers satisfying this condition are -2, -1, 0, 1, 2.
List of elements: C={−2,−1,0,1,2}
(iv) D={x:x is a letter in the word “LOYAL”}
The unique letters in the word “LOYAL” are L, O, Y, and A.
List of elements: D={L,O,Y,A}
(v) E={x:x is a month of a year not having 31 days}
The months of the year that do not have 31 days are February (28 or 29 days), April, June, September, and November (30 days each).
List of elements: E={February, April, June, September, November}
(vi) F={x:x is a consonant in the English alphabet which precedes k}
The consonants that precede “k” in the English alphabet are: B, C, D, F, G, H, J.
List of elements: F={B, C, D, F, G, H, J}
6. Match each of the set on the left in the roster form with the same set on the right described in the set-builder form:
| (i) {1, 2, 3, 6} | (a) {x: x is a prime number and a divisor of 6} |
| (ii) {2, 3} | (b) {x: x is an odd natural number less than 10} |
| (iii) {M, A, T, H, E, I, C, S} | (c) {x: x is a natural number and divisor of 6} |
| (iv) {1, 3, 5, 7, 9} | (d) {x: x is a letter of the word MATHEMATICS} |
Solution:
(i) {1,2,3,6} matches with (c): {x:x is a natural number and divisor of 6}
(ii) {2,3} matches with (a): {x:x is a prime number and a divisor of 6}
(iii) {M,A,T,H,E,I,C,S} matches with (d): {x:x is a letter of the word MATHEMATICS}
(iv) {1,3,5,7,9} matches with (b): {x:x is an odd natural number less than 10}
Exercise 1.2 (Chapter 1 Sets)
1. Which of the following are examples of the null set?
(i) Set of odd natural numbers divisible by 2
(ii) Set of even prime numbers
(iii) {x: x is a natural numbers, x < 5 and x > 7}
(iv) {y: y is a point common to any two parallel lines}
Solution:
(i) Set of odd natural numbers divisible by 2
- The odd natural numbers are numbers like 1, 3, 5, 7, 9, etc. A number is divisible by 2 only if it is even. Therefore, there are no odd numbers that are divisible by 2.
Thus, this set has no elements.
This is an empty set (null set) or ∅
(ii) Set of even prime numbers
- The only even prime number is 2. This is because 2 is divisible by 1 and itself, and it is the only even number that meets the definition of a prime number.
Thus, this set contains one element, which is 2.
This is not an empty set. It contains the element 2.
(iii) {x:x is a natural number,x<5 and x>7}
- The condition specifies that xxx should be both less than 5 and greater than 7. It is impossible for a number to satisfy both conditions at the same time. There is no natural number that is both less than 5 and greater than 7.
Thus, this set has no elements.
This is an empty set (null set) or ∅
(iv) {y:y is a point common to any two parallel lines}
- Two parallel lines never intersect. By definition, parallel lines are always equidistant and do not meet at any point. Therefore, there is no point common to any two parallel lines.
Thus, this set has no elements.
This is an empty set (null set) or ∅
2. Which of the following sets are finite or infinite?
(i) The set of months of a year
(ii) {1, 2, 3 …}
(iii) {1, 2, 3 … 99, 100}
(iv) The set of positive integers greater than 100
(v) The set of prime numbers less than 99
Solution:
(i) The set of months of a year
- A year consists of 12 months: January, February, March, April, May, June, July, August, September, October, November, and December.
This is a finite set, as it has only 12 elements.
(ii) {1,2,3,… }
- This set represents all the natural numbers (i.e., {1,2,3,4,5,6,… }). The natural numbers go on indefinitely without any upper limit.
This is an infinite set, as there is no end to the natural numbers.
(iii) {1,2,3,…,99,100}
- This set contains all the natural numbers from 1 to 100, which is a finite collection of elements.
This is a finite set, as it contains exactly 100 elements.
(iv) The set of positive integers greater than 100
- The set of positive integers greater than 100 includes all integers starting from 101, 102, 103, and so on. There is no upper limit to these integers.
This is an infinite set, as there is no end to the positive integers greater than 100.
(v) The set of prime numbers less than 99
- The prime numbers less than 99 are: 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97.
This is a finite set, as it contains exactly 25 prime numbers.
3. State whether each of the following set is finite or infinite:
(i) The set of lines which are parallel to the x-axis
(ii) The set of letters in the English alphabet
(iii) The set of numbers which are multiple of 5
(iv) The set of animals living on the earth
(v) The set of circles passing through the origin (0, 0)
Solution:
(i) The set of lines which are parallel to the x-axis
- There are infinitely many parallel lines to the x-axis. A line parallel to the x-axis can have any y-intercept, which means that there are an infinite number of such lines.
This is an infinite set because there are infinitely many parallel lines to the x-axis.
(ii) The set of letters in the English alphabet
- The English alphabet consists of exactly 26 letters: A, B, C, D, E, F, G, H, I, J, K, L, M, N, O, P, Q, R, S, T, U, V, W, X, Y, Z.
This is a finite set, as it contains exactly 26 elements.
(iii) The set of numbers which are multiples of 5
- The multiples of 5 include numbers like 5, 10, 15, 20, 25, and so on. There is no upper limit to the multiples of 5; they go on indefinitely.
This is an infinite set, as there are infinitely many multiples of 5.
(iv) The set of animals living on the earth
- The set of animals living on earth is finite in practice, as there are a limited number of animal species living at any given point in time, even though this number may change over time due to extinction or the discovery of new species.
This is a finite set, because the number of animals living on earth is countable and limited at any moment, despite it being a large number.
(v) The set of circles passing through the origin (0, 0)
- A circle passing through the origin has the form x2+y2=r2, where r is the radius. There are infinitely many circles that can pass through the origin, with different radii.
This is an infinite set because there are infinitely many circles passing through the origin with different radii.
4. In the following, state whether A = B or not:
(i) A = {a, b, c, d}; B = {d, c, b, a}
(ii) A = {4, 8, 12, 16}; B = {8, 4, 16, 18}
(iii) A = {2, 4, 6, 8, 10}; B = {x: x is positive even integer and x ≤ 10}
(iv) A = {x: x is a multiple of 10}; B = {10, 15, 20, 25, 30 …}
Solution:
(i) A = {a, b, c, d}; B = {d, c, b, a}
- Set A contains the elements a,b,c,d. Set B also contains the elements d,c,b,a. The order in which elements are listed does not matter in a set, so both sets contain the same elements.
A = B because both sets have the same elements.
(ii) A = {4, 8, 12, 16}; B = {8, 4, 16, 18}
- Set A contains the elements 4,8,12,16. Set B contains the elements 8,4,16,18. Set A contains 12, but Set B does not. Additionally, Set B contains 18, but Set A does not.
A ≠ B because Set A and Set B do not contain the same elements.
(iii) A = {2, 4, 6, 8, 10}; B = {x: x is a positive even integer and x ≤ 10}
- Set A contains the elements 2,4,6,8,10. Set B is defined as the set of all positive even integers less than or equal to 10. This includes 2,4,6,8,10. Both sets contain the same elements.
A = B because both sets have the same elements.
(iv) A = {x: x is a multiple of 10}; B = {10, 15, 20, 25, 30, …}
- Set A is the set of all multiples of 10, i.e., {10,20,30,40,50,… }. Set B contains the elements 10,15,20,25,30,…, which includes the numbers 15 and 25, but 15 and 25 are not multiples of 10. Set B includes elements that are not multiples of 10, so the two sets are not the same.
A ≠ B because Set B contains elements that are not multiples of 10.
5. Are the following pair of sets equal? Give reasons.
(i) A = {2, 3}; B = {x: x is solution of x2+ 5x + 6 = 0}
(ii) A = {x: x is a letter in the word FOLLOW}; B = {y: y is a letter in the word WOLF}
Solution:
(i) A = {2, 3}; B = {x: x is a solution of x2+5x+6=0}
- Set A is given as A={2,3}A = \{ 2, 3 \}A={2,3}, which contains the elements 2 and 3.
- Set B is defined as the set of solutions to the quadratic equation x2+5x+6=0. To find the solutions, we can factor the quadratic expression:
x2+5x+6=0
(x+2)(x+3)=0
This gives us the solutions x=−2 and x=−3.
- So, Set B contains the elements B={−2,−3}
A ≠ B because the elements in Set A ({2, 3}) are different from the elements in Set B ({-2, -3}).
(ii) A = {x: x is a letter in the word “FOLLOW”}; B = {y: y is a letter in the word “WOLF”}
- Set A represents the letters in the word “FOLLOW”. The letters in the word “FOLLOW” are: F, O, L, L, O, W. So, Set A is A={F,O,L,W}. Set B represents the letters in the word “WOLF”. The letters in the word “WOLF” are: W, O, L, F. As there are no duplicates, Set B is B={W,O,L,F}B = \{ W, O, L, F \}B={W,O,L,F}.
- Both sets A and B contain the exact same elements: F, O, L, W.
A = B because both sets contain the same elements. A = B
6. From the sets given below, select equal sets:
A = {2, 4, 8, 12}, B = {1, 2, 3, 4}, C = {4, 8, 12, 14}, D = {3, 1, 4, 2}
E = {–1, 1}, F = {0, a}, G = {1, –1}, H = {0, 1}
Solution:
1. A = {2, 4, 8, 12}
- Set A contains the elements: 2,4,8,12.
2. B = {1, 2, 3, 4}
- Set B contains the elements: 1,2,3,4.
- The elements in Set A are different from those in Set B.
A ≠ B
3. C = {4, 8, 12, 14}
- Set C contains the elements: 4,8,12,14.
- The elements in Set A and Set C are not the same (e.g., Set A contains 2 and Set C contains 14).
A ≠ C
4. D = {3, 1, 4, 2}
- Set D contains the elements: 3,1,4,2.
- Set D has the same elements as Set B, but in a different order. Since order does not matter in sets.
D = B.
5. E = {-1, 1}
- Set E contains the elements: −1,1-1, 1−1,1.
6. F = {0, a}
- Set F contains the elements: 0,a0, a0,a.
E ≠ F because Set E contains −1,1 and Set F contains 0,a.
7. G = {1, -1}
- Set G contains the elements: 1,−1.
E = G because both sets contain the elements −1 and 1, but the order doesn’t matter.
8. H = {0, 1}
- Set H contains the elements: 0,1.
E ≠ H because Set E contains −1, and Set H does not.
Exercise 1.3 (Chapter 1 Sets)
1. Make correct statements by filling in the symbols ⊂ or ⊄ in the blank spaces:
(i) {2, 3, 4} … {1, 2, 3, 4, 5}
(ii) {a, b, c} … {b, c, d}
(iii) {x: x is a student of Class XI of your school} … {x: x student of your school}
(iv) {x: x is a circle in the plane} … {x: x is a circle in the same plane with radius 1 unit}
(v) {x: x is a triangle in a plane}…{x: x is a rectangle in the plane}
(vi) {x: x is an equilateral triangle in a plane}… {x: x is a triangle in the same plane}
(vii) {x: x is an even natural number} … {x: x is an integer}
Solution:
(i) {2, 3, 4} ⊂ {1, 2, 3, 4, 5}
(ii) {a, b, c} ⊄ {b, c, d}
(iii) {x: x is a student of Class XI of your school} ⊂ {x: x is a student of your school}
(iv) {x: x is a circle in the plane} ⊄ {x: x is a circle in the same plane with radius 1 unit}
(v) {x: x is a triangle in a plane} ⊄ {x: x is a rectangle in the plane}
(vi) {x: x is an equilateral triangle in a plane} ⊂ {x: x is a triangle in the same plane}
(vii) {x: x is an even natural number} ⊂ {x: x is an integer}
2. Examine whether the following statements are true or false:
(i) {a, b} ⊄ {b, c, a}
(ii) {a, e} ⊂ {x: x is a vowel in the English alphabet}
(iii) {1, 2, 3} ⊂ {1, 3, 5}
(iv) {a} ⊂ {a. b, c}
(v) {a} ∈ (a, b, c)
(vi) {x: x is an even natural number less than 6} ⊂ {x: x is a natural number which divides 36}
Solution:
(i) {a, b} ⊄ {b, c, a}
False, {a, b} is a subset of {b, c, a} because both a and b are contained in {b, c, a}. The symbol ⊄ means “is not a subset”, but in this case, {a, b} is indeed a subset, so the statement is false.
(ii) {a, e} ⊂ {x: x is a vowel in the English alphabet}
True, The set {a, e} is a subset of the set of vowels in the English alphabet {a, e, i, o, u} because both a and e are vowels and are included in the larger set.
(iii) {1, 2, 3} ⊂ {1, 3, 5}
False, {1, 2, 3} is not a subset of {1, 3, 5} because 2 is present in {1, 2, 3} but not in {1, 3, 5}. Hence, it is not a subset.
(iv) {a} ⊂ {a, b, c}
True, {a} is a subset of {a, b, c} because a is an element of the set {a, b, c}, so it qualifies as a subset.
(v) {a} ∈ (a, b, c)
False, {a} is a set containing a, and (a, b, c) is a list (not a set) of elements a, b, and c. A set {a} is not an element of this list, so the statement is false.
(vi) {x: x is an even natural number less than 6} ⊂ {x: x is a natural number which divides 36}
True, The set {2, 4} of even natural numbers less than 6 is a subset of the set of divisors of 36 ({1, 2, 3, 4, 6, 9, 12, 18, 36}) because both 2 and 4 divides 36. Hence, the statement is true.
3. Let A= {1, 2, {3, 4}, 5}. Which of the following statements are incorrect and why?
(i) {3, 4} ⊂ A
(ii) {3, 4}∈ A
(iii) {3, 4} ⊂ A
(iv) 1 ∈ A
(v) 1⊂ A
(vi) {1, 2, 5} ⊂ A
(vii) {1, 2, 5} ∈ A
(viii) {1, 2, 3} ⊂ A
(ix) Φ ∈ A
(x) Φ ⊂ A
(xi) {Φ} ⊂ A
Solution:
(i) {3, 4} ⊂ A
Incorrect, {3, 4} is not a subset of A because A contains {3, 4} as an element, but not as an individual element like 3 and 4. A subset would require that each element of {3, 4} (i.e., 3 and 4) must also be in A, but 3 and 4 are not directly present in A as individual elements.
(ii) {3, 4} ∈ A
Correct, {3, 4} is an element of A because A explicitly contains the set {3, 4} as an element.
(iii) {3, 4} ⊂ A
Correct, {3, 4} is a set containing the set 3 and 4 is indeed an element of A. Hence, {3, 4}}is a subset of A because it only contains one element, which is {3, 4}, and that element is in A.
(iv) 1 ∈ A
Correct, 1 is an element of A, as we can see from the set A = {1, 2, {3, 4}, 5}.
(v) 1 ⊂ A
Incorrect, 1 is not a set; it is an element of A. The symbol ⊂ denotes “subset,” which is only applicable to sets. Since 1 is not a set, it cannot be a subset of A.
(vi) {1, 2, 5} ⊂ A
Correct, The set {1, 2, 5} is a subset of A because all its elements 1, 2, and 5 are elements of A.
(vii) {1, 2, 5} ∈ A
Incorrect, {1, 2, 5} is not an element of A. A contains 1, 2, {3, 4}, and 5 as elements, but not the set {1, 2, 5} itself.
(viii) {1, 2, 3} ⊂ A
Incorrect, {1, 2, 3} is not a subset of A because 3 is not an element of A (although {3, 4} is an element of A, 3 itself is not).
(ix) Φ ∈ A
Incorrect, Φ (the empty set) is not an element of A. A contains 1, 2, {3, 4}, 5, but not the empty set Φ as an element.
(x) Φ ⊂ A
Correct, The empty set Φ is a subset of every set, including A, because the empty set does not contain any elements that could contradict the condition of being a subset.
(xi) {Φ} ⊂ A
Incorrect, {Φ} is a set containing the empty set Φ as its only element. Since Φ is not an element of A, the set {Φ} is not a subset of A.
4. Write down all the subsets of the following sets:
(i) {a}
(ii) {a, b}
(iii) {1, 2, 3}
(iv) Φ
Solution:
(i) {a}
The set {a} has only two subsets: Φ (The empty set) and {a} (The set itself)
(ii) {a, b}
The set {a, b} has 4 subsets. This is because the number of subsets of a set with n elements is given by 2n. Here, n=2, so there are 22=4 subsets.
Subsets of {a, b}: Φ (The empty set), {a} (A subset with element a), {b} (A subset with element b) and {a, b} (The set itself)
(iii) {1, 2, 3}
The set {1, 2, 3} has 8 subsets, since 23=8.
Subsets of {1, 2, 3}: Φ (The empty set), {1} (A subset with element 1), {2} (A subset with element 2), {3} (A subset with element 3), {1, 2} (A subset with elements 1 and 2), {1, 3} (A subset with elements 1 and 3), {2, 3} (A subset with elements 2 and 3) and{1, 2, 3} (The set itself).
(iv) Φ (Empty set)
The empty set Φ has 1 subset, which is itself: the empty set.
Subsets of Φ: Φ (The empty set itself)
5. How many elements has P (A), if A = Φ?
Solution:
P(Φ) has 1 element (the empty set).
6. Write the following as intervals:
(i) {x: x ∈ R, –4 < x ≤ 6}
(ii) {x: x ∈ R, –12 < x < –10}
(iii) {x: x ∈ R, 0 ≤ x < 7}
(iv) {x: x ∈ R, 3 ≤ x ≤ 4}
Solution:
(i) {x: x ∈ R, –4 < x ≤ 6}
This set includes all real numbers greater than -4 but less than or equal to 6.
Interval notation: (−4,6]
(ii) {x: x ∈ R, –12 < x < –10}
This set includes all real numbers between -12 and -10, but not including -12 or -10 themselves.
Interval notation: (−12,−10)
(iii) {x: x ∈ R, 0 ≤ x < 7}
This set includes all real numbers from 0 to 7, including 0, but not 7.
Interval notation: [0,7
(iv) {x: x ∈ R, 3 ≤ x ≤ 4}
This set includes all real numbers from 3 to 4, including both 3 and 4.
Interval notation: [3,4]
7. Write the following intervals in set-builder form:
(i) (–3, 0)
(ii) [6, 12]
(iii) (6, 12]
(iv) [–23, 5)
Solution:
(i) (–3, 0)
This interval represents all numbers greater than -3 but less than 0.
In set-builder form, we can write it as: {x:−3<x<0}
(ii) [6, 12]
This interval includes all numbers from 6 to 12, including both 6 and 12.
In set-builder form, we can write it as: {x:6≤x≤12}
(iii) (6, 12]
This interval represents all numbers greater than 6 but less than or equal to 12.
In set-builder form, we can write it as: {x:6<x≤12}
(iv) [–23, 5)
This interval includes all numbers from -23 to 5, including -23 but not including 5.
In set-builder form, we can write it as: {x:−23≤x<5}
8. What universal set (s) would you propose for each of the following?
(i) The set of right triangles
(ii) The set of isosceles triangles
Solution:
(i) The set of right triangles
The set of right triangles consists of all triangles where one angle is exactly 90°. To define this set properly, the universal set should be all possible triangles, because right triangles are a subset of the larger category of triangles.
Proposed universal set: U={All triangles}
(ii) The set of isosceles triangles
The set of isosceles triangles includes all triangles where at least two sides are of equal length.
The universal set for this category should again be the set of all triangles since isosceles triangles are a specific type of triangle.
Proposed universal set: U={All triangles}
9. Given the sets A = {1, 3, 5}, B = {2, 4, 6} and C = {0, 2, 4, 6, 8}, which of the following may be considered as universals set (s) for all the three sets A, B and C?
(i) {0, 1, 2, 3, 4, 5, 6}
(ii) Φ
(iii) {0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10}
(iv) {1, 2, 3, 4, 5, 6, 7, 8}
Solution:
O(i): {0,1,2,3,4,5,6}
This set contains the elements 0,1,2,3,4,5,6 but it does not include 8, which is part of set C.
Hence, this is not a valid universal set for all three sets.
(ii): Φ (Empty set)
The empty set contains no elements, and since all the sets A, B, and C have elements, the empty set cannot be a universal set.
This is incorrect.
(iii): {0,1,2,3,4,5,6,7,8,9,10}
This set contains all the elements in sets A, B, and C and also includes additional elements like 7, 9, and 10. Since it encompasses all the elements of A, B, and C, this is a valid universal set. It includes the complete set of elements that can be considered in the context of these sets.
(iv): {1,2,3,4,5,6,7,8}
This set contains all elements except 0, part of set C. Since it does not contain the element 0, this cannot be a valid universal set.
This is incorrect.
Exercise 1.4 (Chapter 1 Sets)
1. Find the union of each of the following pairs of sets:
(i) X = {1, 3, 5} Y = {1, 2, 3}
(ii) A = {a, e, i, o, u} B = {a, b, c}
(iii) A = {x: x is a natural number and multiple of 3}
B = {x: x is a natural number less than 6}
(iv) A = {x: x is a natural number and 1 < x ≤ 6}
B = {x: x is a natural number and 6 < x < 10}
(v) A = {1, 2, 3}, B = Φ
Solution:
(i) Union of X and Y:
- X={1,3,5} and Y={1,2,3}
X∪Y={1,2,3,5}
(ii) Union of A and B:
- A={a,e,i,o,u} and B={a,b,c}
A∪B={a,b,c,e, i,o,u}
(iii) Union of A and B:
- A={x:x is a natural number and multiple of 3} and B={x:x is a natural number less than 6}
A∪B={1,2,3,4,5}
(iv) Union of AAA and BBB:
- A={x:x is a natural number and 1<x≤6} and B={x:x is a natural number and 6<x<10}
A∪B={2,3,4,5,6,7,8,9}
(v) Union of AAA and BBB:
- A={1,2,3} and B=Φ
A∪B={1,2,3}
2. Let A = {a, b}, B = {a, b, c}. Is A ⊂ B? What is A ∪ B?
Solution:
A⊂B is True.
A∪B={a,b,c}
3. If A and B are two sets such that A ⊂ B, then what is A ∪ B?
Solution:
If A and B are two sets such that A ⊂ B, then A ∪ B = B.
4. If A = {1, 2, 3, 4}, B = {3, 4, 5, 6}, C = {5, 6, 7, 8} and D = {7, 8, 9, 10}; find
(i) A ∪ B
(ii) A ∪ C
(iii) B ∪ C
(iv) B ∪ D
(v) A ∪ B ∪ C
(vi) A ∪ B ∪ D
(vii) B ∪ C ∪ D
Solution:
(i) A∪B={1,2,3,4}∪{3,4,5,6}={1,2,3,4,5,6}
(ii) A∪C={1,2,3,4}∪{5,6,7,8}={1,2,3,4,5,6,7,8}
(iii) B∪C={3,4,5,6}∪{5,6,7,8}={3,4,5,6,7,8}
(iv) B∪D={3,4,5,6}∪{7,8,9,10}={3,4,5,6,7,8,9,10}
(v) A∪B∪C={1,2,3,4}∪{3,4,5,6}∪{5,6,7,8}={1,2,3,4,5,6,7,8}
(vi) A∪B∪D={1,2,3,4}∪{3,4,5,6}∪{7,8,9,10}={1,2,3,4,5,6,7,8,9,10}
(vii) B∪C∪D={3,4,5,6}∪{5,6,7,8}∪{7,8,9,10}={3,4,5,6,7,8,9,10}
5. Find the intersection of each pair of sets:
(i) X = {1, 3, 5} Y = {1, 2, 3}
(ii) A = {a, e, i, o, u} B = {a, b, c}
(iii) A = {x: x is a natural number and multiple of 3}
B = {x: x is a natural number less than 6}
(iv) A = {x: x is a natural number and 1 < x ≤ 6}
B = {x: x is a natural number and 6 < x < 10}
(v) A = {1, 2, 3}, B = Φ
Solution:
(i) X∩Y={1,3}
(ii) A∩B={a}
(iii) A∩B={3}
(iv) A∩B=∅
(v) A∩B=∅
6. If A = {3, 5, 7, 9, 11}, B = {7, 9, 11, 13}, C = {11, 13, 15} and D = {15, 17}; find
(i) A ∩ B
(ii) B ∩ C
(iii) A ∩ C ∩ D
(iv) A ∩ C
(v) B ∩ D
(vi) A ∩ (B ∪ C)
(vii) A ∩ D
(viii) A ∩ (B ∪ D)
(ix) (A ∩ B) ∩ (B ∪ C)
(x) (A ∪ D) ∩ (B ∪ C)
Solution:
(i) A∩B):
The intersection of two sets includes the elements that are present in both sets.
A={3,5,7,9,11}, B={7,9,11,13}
Common elements are 7,9,11.
A∩B={7,9,11}
(ii) B∩C:
We find the common elements between B={7,9,11,13} and C={11,13,15}.
The common elements are 11,13.
B∩C={11,13}
(iii) A∩B∩C∩D
We need to find the common elements between all four sets:
A={3,5,7,9,11},B={7,9,11,13},C={11,13,15},D={15,17}
Since there are no elements common to all four sets, the intersection is the empty set.
A∩B∩C∩D=∅
(iv) A∩C:
We find the common elements between A={3,5,7,9,11} and C={11,13,15}.
The common element is 11.
A∩C={11}
(v) B∩D:
We find the common elements between B={7,9,11,13} and D={15,17}.
There are no common elements.
B∩D=∅
(vi) A∩(B∪C):
First, we find the union of B and C:
B∪C={7,9,11,13,15}
Now, we find the intersection of A={3,5,7,9,11} with B∪C={7,9,11,13,15}.
The common elements are 7,9,11.
A∩(B∪C)={7,9,11}
(vii) A∩DA:
We find the common elements between A={3,5,7,9,11} and D={15,17}.
There are no common elements.
A∩D=∅
(viii) A∩(B∪D):
First, find the union of B and D:
B∪D={7,9,11,13,15,17}
Now, find the intersection of A={3,5,7,9,11} with B∪D={7,9,11,13,15,17}.
The common elements are 7,9,11.
A∩(B∪D)={7,9,11}
(ix) (A∩B)∩(B∪C):
From part (i), we know that:
A∩B={7,9,11}A \cap B = \{7, 9, 11\}A∩B={7,9,11}
From part (ii), we know that:
B∪C={7,9,11,13,15}
Now, find the intersection of A∩B={7,9,11} with B∪C={7,9,11,13,15}.
The common elements are 7,9,11.
(A∩B)∩(B∪C)={7,9,11}
(x) (A∪D)∩(B∪C):
First, find the union of A and D:
A∪D={3,5,7,9,11,15,17}
Now, find the union of B and C:
B∪C={7,9,11,13,15}
Now, find the intersection of A∪D={3,5,7,9,11,15,17 with B∪C={7,9,11,13,15}.
The common elements are 7,9,11,15.
(A∪D)∩(B∪C)={7,9,11,15}
7. If A = {x: x is a natural number}, B ={x: x is an even natural number}
C = {x: x is an odd natural number} and D = {x: x is a prime number}, find
(i) A ∩ B
(ii) A ∩ C
(iii) A ∩ D
(iv) B ∩ C
(v) B ∩ D
(vi) C ∩ D
Solution:
(i) A∩B:
The set A is the set of all natural numbers, and the set B consists of all even natural numbers. The intersection A∩B will be the set of even natural numbers, as every even number is a natural number.
A∩B=B={2,4,6,8,10,12,… }
(ii) A∩C:
The set A is the set of all natural numbers, and the set C consists of all odd natural numbers. The intersection A∩C will be the set of odd natural numbers, as every odd number is a natural number.
A∩C=C={1,3,5,7,9,11,… }
(iii) A∩D:
The set A is the set of all natural numbers, and the set D consists of all prime numbers. The intersection A∩DA will be the set of all prime numbers, as every prime number is a natural number.
A∩D=D={2,3,5,7,11,13,17,19,23,… }
(iv) B∩CB:
The set B consists of all even natural numbers, and the set C consists of all odd natural numbers. Since there are no numbers that are both even and odd, the intersection is the empty set.
B∩C=∅
(v) B∩D):
The set B consists of all even natural numbers and the set D consists of all prime numbers. The only even prime number is 222, so the intersection will be:
B∩D={2}
(vi) C∩D:
The set C consists of all odd natural numbers, and the set D consists of all prime numbers. The odd prime numbers are 3,5,7,11,13,17,19,… So, the intersection will be the set of odd prime numbers.
C∩D={3,5,7,11,13,17,19,… }
8. Which of the following pairs of sets are disjoint?
(i) {1, 2, 3, 4} and {x: x is a natural number and 4 ≤ x ≤ 6}
(ii) {a, e, i, o, u}and {c, d, e, f}
(iii) {x: x is an even integer} and {x: x is an odd integer}
Solution:
(i) {1, 2, 3, 4} and {x: x is a natural number and 4 ≤ x ≤ 6}
- The first set is {1, 2, 3, 4}. The second set is {x: x is a natural number and 4 ≤ x ≤ 6}, which can be written as {4, 5, 6}.
Intersection of these sets: The common element between {1, 2, 3, 4} and {4, 5, 6} is 4.
Since the sets have a common element, they are not disjoint.
(ii) {a, e, i, o, u} and {c, d, e, f}
- The first set is {a, e, i, o, u} (vowels). The second set is {c, d, e, f}.
Intersection of these sets: The common element between {a, e, i, o, u} and {c, d, e, f} is e.
Since the sets have a common element, they are not disjoint.
(iii) {x: x is an even integer} and {x: x is an odd integer}
- The first set is {x: x is an even integer} (which includes numbers like 2, 4, 6, -2, -4, etc.). The second set is {x: x is an odd integer} (which includes numbers like 1, 3, 5, -1, -3, etc.).
Intersection of these sets: There are no integers that are both even and odd. The sets do not share any common elements.
Since there are no common elements, these sets are disjoint.
9. If A = {3, 6, 9, 12, 15, 18, 21}, B = {4, 8, 12, 16, 20},
C = {2, 4, 6, 8, 10, 12, 14, 16}, D = {5, 10, 15, 20}; find
(i) A – B
(ii) A – C
(iii) A – D
(iv) B – A
(v) C – A
(vi) D – A
(vii) B – C
(viii) B – D
(ix) C – B
(x) D – B
(xi) C – D
(xii) D – C
Solution:
(i) A – B
To find A−B, we subtract the elements of B from A.
- A = {3,6,9,12,15,18,21} and B = {4,8,12,16,20}\
Elements of A that are not in B: 3,6,9,15,18,21
Answer: A−B={3,6,9,15,18,21}
(ii) A – C
To find A−C, we subtract the elements of C from A.
- A = {3,6,9,12,15,18,21} and C = {2,4,6,8,10,12,14,16}
Elements of A that are not in C: 3,9,15,18,21
Answer: A−C={3,9,15,18,21}
(iii) A – D
To find A−D, we subtract the elements of D from A.
- A = {3,6,9,12,15,18,21} and D = {5,10,15,20}
Elements of A that are not in D: 3,6,9,12,18,21
Answer: A−D={3,6,9,12,18,21}
(iv) B – A
To find B−A, we subtract the elements of A from B.
- B = {4,8,12,16,20} and A = {3,6,9,12,15,18,21}
Elements of B that are not in A: 4,8,16,20
Answer: B−A={4,8,16,20}
(v) C – A
To find C−A, we subtract the elements of A from C.
- C = {2,4,6,8,10,12,14,16} and A = {3,6,9,12,15,18,21}
Elements of C that are not in A: 2,4,8,10,14,16
Answer: C−A={2,4,8,10,14,16}
(vi) D – A
To find D−A, we subtract the elements of A from D.
- D = {5,10,15,20} and A = {3,6,9,12,15,18,21}
Elements of D that are not in A: 5,10,20
Answer: D−A={5,10,20}
(vii) B – C
To find B−C, we subtract the elements of C from B.
- B = {4,8,12,16,20} and C = {2,4,6,8,10,12,14,16}
Elements of B that are not in C: 20
Answer: B−C={20}
(viii) B – D
To find B−D, we subtract the elements of D from B.
- B = {4,8,12,16,20} and D = {5,10,15,20}
Elements of B that are not in D: 4,8,12,16
Answer: B−D={4,8,12,16}
(ix) C – B
To find C−−B, we subtract the elements of B from C.
- C = {2,4,6,8,10,12,14,16}
- B = {4,8,12,16,20}
Elements of C that are not in B: 2,6,10,14
Answer: C−B={2,6,10,14}
(x) D – B
To find D−B, we subtract the elements of B from D.
- D = {5,10,15,20} and B = {4,8,12,16,20}
Elements of D that are not in B: 5,10,15
Answer: D−B={5,10,15}
(xi) C – D
To find C−D, we subtract the elements of D from C.
- C = {2,4,6,8,10,12,14,16} and D = {5,10,15,20}
Elements of C that are not in D: 2,4,6,8,12,14,16
Answer: C−D={2,4,6,8,12,14,16}
(xii) D – C
To find D−C, we subtract the elements of C from D.
- D = {5,10,15,20}
- C = {2,4,6,8,10,12,14,16}
Elements of D that are not in C: 5,15,20
Answer: D−C={5,15,20}
11. If R is the set of real numbers and Q is the set of rational numbers, then what is R – Q?
Solution:
R−Q represents the set of real numbers that are not rational. These are the irrational numbers.
R−Q=Set of all irrational numbers or R−Q={x∈R∣x∉Q}
12. State whether each of the following statement is true or false. Justify your answer.
(i) {2, 3, 4, 5} and {3, 6} are disjoint sets.
(ii) {a, e, i, o, u } and {a, b, c, d} are disjoint sets.
(iii) {2, 6, 10, 14} and {3, 7, 11, 15} are disjoint sets.
(iv) {2, 6, 10} and {3, 7, 11} are disjoint sets.
Solution:
(i) False – The sets {2,3,4,5} and {3,6} are not disjoint because they have a common element (3).
(ii) False – The sets {a,e,i,o,u} and {a,b,c,d} are not disjoint because they have a common element (a).
(iii) True – The sets {2,6,10,14} and {3,7,11,15} are disjoint because they have no common elements.
(iv) True – The sets {2,6,10} and {3,7,11} are disjoint because they have no common elements.
Exercise 1.5 (Chapter 1 Sets)
1. Let U = {1, 2, 3; 4, 5, 6, 7, 8, 9}, A = {1, 2, 3, 4}, B = {2, 4, 6, 8} and C = {3, 4, 5, 6}. Find
(i) A’
(ii) B’
(iii) (A U C)’
(iv) (A U B)’
(v) (A’)’
(vi) (B – C)’
Solution:
We are given the following sets:
- Universal Set (U) = {1,2,3,4,5,6,7,8,9}
- Set A = {1,2,3,4}
- Set B = {2,4,6,8}
- Set C = {3,4,5,6}
(i) A′ (Complement of A)
The complement of A (A′) is the set of all elements in the universal set U that are not in A.
- Set A = {1,2,3,4}
Thus, the elements of A′ are the elements of U that are not in A.
- U={1,2,3,4,5,6,7,8,9}
- Elements not in A are: 5,6,7,8,9
Therefore,
A′={5,6,7,8,9}
(ii) B′ (Complement of B)
The complement of B (‘B′) is the set of all elements in U that are not in B.
- Set B = {2,4,6,8}
Thus, the elements of B′ are the elements of U that are not in B.
- U={1,2,3,4,5,6,7,8,9}
- Elements not in B are: 1,3,5,7,9
Therefore,
B′={1,3,5,7,9}
(iii) (A∪C)′ (Complement of A∪CA)
The union of sets A and C is the set of all elements that are in A or in C (or both).
- Set A = {1,2,3,4} and Set C = {3,4,5,6}
The union of A and C is:
A∪C={1,2,3,4,5,6}
Now, the complement of A∪CA ((A∪C)′) is the set of all elements in U that are not in A∪C.
- U={1,2,3,4,5,6,7,8,9}
- Elements not in A∪C are: 7,8,9
Therefore,
(A∪C)′={7,8,9}
(iv) (A∪B)′
The union of sets A and B is the set of all elements that are in A or in B (or both).
- Set A = {1,2,3,4} and Set B = {2,4,6,8}
The union of A and B is:
A∪B={1,2,3,4,6,8}
Now, the complement of A∪B ((A∪B)′) is the set of all elements in U that are not in A∪B.
- U={1,2,3,4,5,6,7,8,9}
- Elements not in A∪B are: 5,7,9
Therefore,
(A∪B)′={5,7,9}
(v) (A′)′ (Complement of the complement of A)
The complement of A′ is simply the set A itself because the complement of the complement of a set gives the original set.
Thus,
(A′)′=A={1,2,3,4}
(vi) (B−C)′ (Complement of the set difference B−C)
The set difference B−C consists of all elements in B that are not in C.
- Set B = {2,4,6,8}
- Set C = {3,4,5,6}
The set difference B−C is:
B−C={2,8}
Now, the complement of B−C ((B−C)′) is the set of all elements in U that are not in B−C.
- U={1,2,3,4,5,6,7,8,9}
- Elements not in {2,8} are: 1,3,4,5,6,7,9
Therefore,
(B−C)′={1,3,4,5,6,7,9}
2. If U = {a, b, c, d, e, f, g, h}, find the complements of the following sets:
(i) A = {a, b, c}
(ii) B = {d, e, f, g}
(iii) C = {a, c, e, g}
(iv) D = {f, g, h, a}
Solution:
We are given the Universal Set U={a,b,c,d,e,f,g,h} and are asked to find the complements of the following sets:
- Set A = {a,b,c}
- Set B = {d,e,f,g}
- Set C = {a,c,e,g}
- Set D = {f,g,h,a}
(i) Complement of Set A (A′)
- Set A = {a,b,c}
- Universal Set (U) = {a,b,c,d,e,f,g,h}
The complement of A (A′) is the set of elements in U that are not in A.
- Elements not in {a,b,c} are: d,e,f,g,h
Therefore,
A′={d,e,f,g,h}
(ii) Complement of Set B (B′)
- Set B = {d,e,f,g}
- Universal Set (U) = {a,b,c,d,e,f,g,h}
The complement of B (B′) is the set of elements in U that are not in B.
- Elements not in {d,e,f,g} are: a,b,c,h
Therefore,
B′={a,b,c,h}
(iii) Complement of Set C (C′)
- Set C = {a,c,e,g}
- Universal Set (U) = {a,b,c,d,e,f,g,h}
The complement of C (C′) is the set of elements in U that are not in C.
- Elements not in {a,c,e,g} are: b,d,f,h
Therefore,
C′={b,d,f,h}
(iv) Complement of Set D (D′)
- Set D = {f,g,h,a}
- Universal Set (U) = {a,b,c,d,e,f,g,h}
The complement of D (D′) is the set of elements in U that are not in D.
- Elements not in {f,g,h,a} are: b,c,d,e
Therefore,
D′={b,c,d,e}
3. Taking the set of natural numbers as the universal set, write down the complements of the following sets:
(i) {x: x is an even natural number}
(ii) {x: x is an odd natural number}
(iii) {x: x is a positive multiple of 3}
(iv) {x: x is a prime number}
(v) {x: x is a natural number divisible by 3 and 5}
(vi) {x: x is a perfect square}
(vii) {x: x is perfect cube}
(viii) {x: x + 5 = 8}
(ix) {x: 2x + 5 = 9}
(x) {x: x ≥ 7}
(xi) {x: x ∈ N and 2x + 1 > 10}
Solution:
(i) Complement of {x:x is an even natural number}={x:x is an odd natural number}
(ii) Complement of {x:x is an odd natural number}={x:x is an even natural number}
(iii) Complement of {x:x is a positive multiple of 3}={x:x is not divisible by 3}
(iv) Complement of {x:x is a prime number}={x:x is not a prime number}
(v) Complement of {x:x is a natural number divisible by 3 and 5}={x:x is not divisible by both 3 and 5
(vi) Complement of {x:x is a perfect square}={x:x is not a perfect square}
(vii) Complement of {x:x is a perfect cube}={x:x is not a perfect cube}\
(viii) Complement of {x:x+5=8}=N−{3}
(ix) Complement of {x:2x+5=9}=N−{2}
(x) Complement of {x:x≥7}={1,2,3,4,5,6}
(xi) Complement of {x:x∈N and 2x+1>10}={1,2,3,4}
4. If U = {1, 2, 3, 4, 5,6,7,8, 9}, A = {2, 4, 6, 8} and B = {2, 3, 5, 7}. Verify that
(i) (A U B)’ = A’ ∩ B’
(ii) (A ∩ B)’ = A’ U B’
Solution:
Given:
- Universal Set (U): U={1,2,3,4,5,6,7,8,9}
- Set A: A={2,4,6,8}
- Set B: B={2,3,5,7}
(i) Verifying (A∪B)′=A′∩B′
Step 1: Find A∪BA (Union of A and B):
The union of two sets A and B is the set of all elements that are in A or in B or in both.
A∪B={2,4,6,8}∪{2,3,5,7}={2,3,4,5,6,7,8}
Step 2: Find (A∪B)′ (Complement of A∪B):
The complement of A∪B is the set of elements in U that are not in A∪B.
(A∪B)′=U−(A∪B)={1,2,3,4,5,6,7,8,9}−{2,3,4,5,6,7,8}={1,9}
Step 3: Find A′ and B′ (Complements of A and B):
- A′ is the complement of A, i.e., the set of elements in U that are not in A:
A′=U−A={1,2,3,4,5,6,7,8,9}−{2,4,6,8}={1,3,5,7,9}
- B′ is the complement of B, i.e., the set of elements in U that are not in B:
B′=U−B={1,2,3,4,5,6,7,8,9}−{2,3,5,7}={1,4,6,8,9}
Step 4: Find A′∩B′ (Intersection of A′ and B′):
The intersection of two sets A′ and B′ is the set of all elements that are in both A′ and B′.
A′∩B′={1,3,5,7,9}∩{1,4,6,8,9}={1,9}
Step 5: Compare (A∪B) and A′∩B′:
From the above steps, we have:
(A∪B)′={1,9}
Since (A∪B)′=A′∩B′, this verifies that the first identity is true.
(ii) Verifying (A∩B)′=A′∪B′
Step 1: Find A∩B (Intersection of A and B):
The intersection of two sets A and B is the set of all elements that are in both A and B.
A∩B={2,4,6,8}∩{2,3,5,7}={2}
Step 2: Find (A∩B)′ (Complement of A∩BA \cap BA∩B):
The complement of A∩BA is the set of elements in U that are not in A∩B.
(A∩B)′=U−(A∩B)={1,2,3,4,5,6,7,8,9}−{2}={1,3,4,5,6,7,8,9}
Step 3: Find A′∪B′ (Union of A′ and B′):
- A′={1,3,5,7,9}
- B′={1,4,6,8,9}
The union of A′ and B’ is the set of all elements that are in either A′ or B′ or in both:
A′∪B′={1,3,5,7,9}∪{1,4,6,8,9}={1,3,4,5,6,7,8,9}
Step 4: Compare (A∩B)′ and A′∪B′:
From the above steps, we have:
(A∩B)′={1,3,4,5,6,7,8,9}
A′∪B′={1,3,4,5,6,7,8,9}
Since (A∩B)′=A′∪B′, this verifies that the second identity is true.
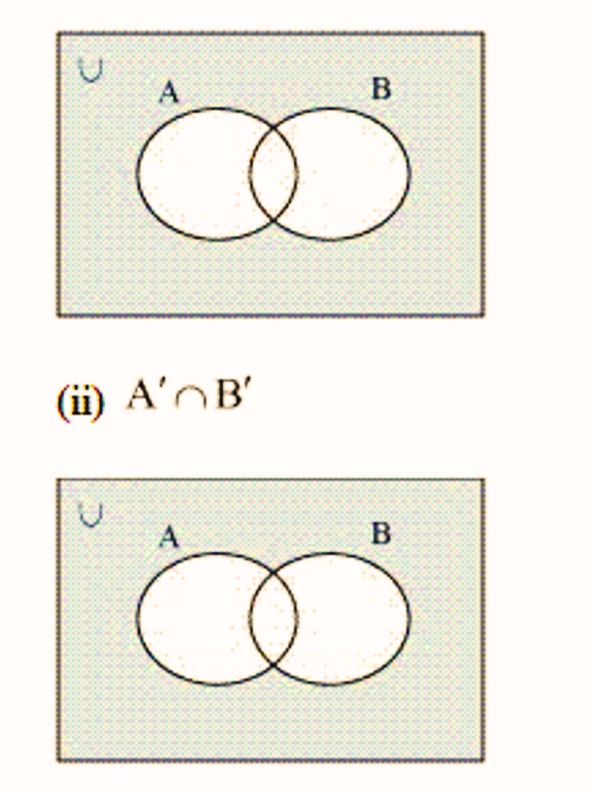
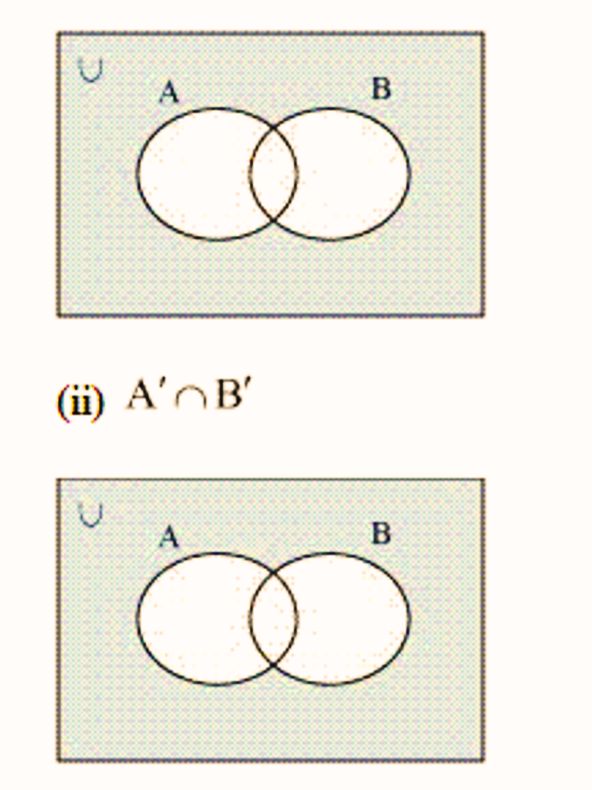
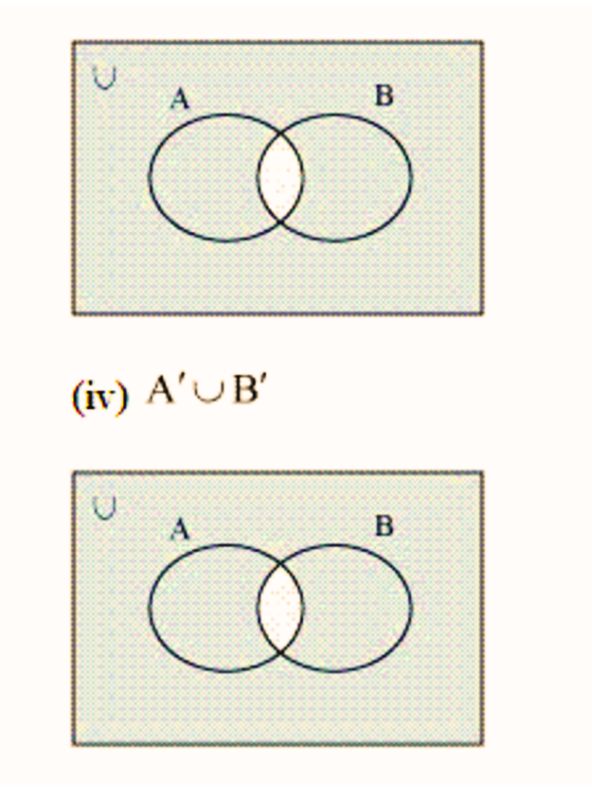
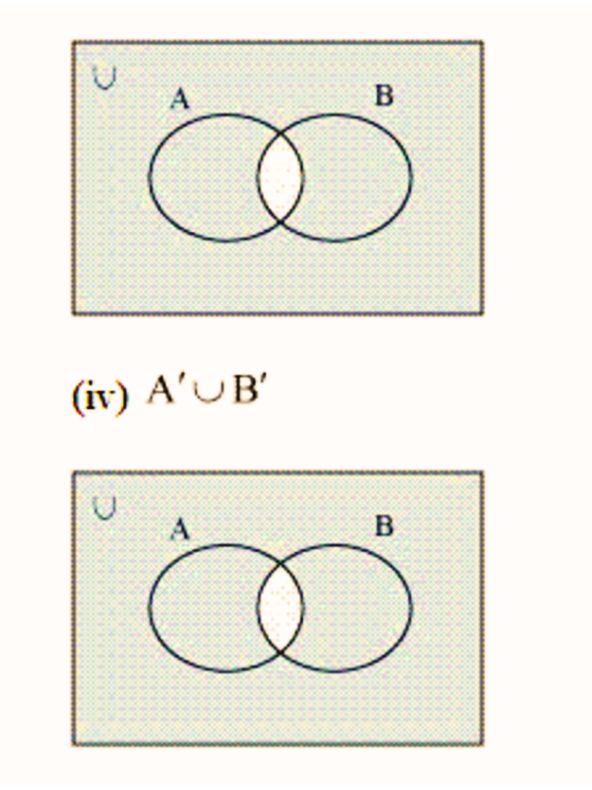
5. Draw appropriate Venn diagram for each of the following:
(i) (A U B)’
(ii) A’ ∩ B’
(iii) (A ∩ B)’
(iv) A’ U B’
Solution:
(i) (A U B)’
(ii) A’ ∩ B’
(iii) (A ∩ B)’
(iv) A’ U B’
6. Let U be the set of all triangles in a plane. If A is the set of all triangles with at least one angle different from 60°, what is A’?
Solution:
The set A′, the complement of A, is the set of all equilateral triangles, where all three angles are 60°.
A′={Equilateral triangles}
7. Fill in the blanks to make each of the following a true statement:
(i) A U A’ = ……..
(ii) Φ′ ∩ A = …….
(iii) A ∩ A’ = …….
(iv) U’ ∩ A = …….
Solution:
(i) A∪A′=…
- Explanation: A′ is the complement of A, meaning all the elements in the universal set U that are not in A. The union of A and A′ includes all elements of A and all elements of A′, which together cover the entire universal set U.
Answer: A∪A′=U
(ii) Φ′∩A=…
- Explanation: Φ is the empty set, so Φ′ is the complement of the empty set. The complement of the empty set is the entire universal set U. The intersection of U with any set A is just A, because A is a subset of U.
Answer: Φ′∩A=A
(iii) A∩A′=…
- Explanation: A∩A′ represents the intersection of a set A and its complement A′. Since A and A′ have no common elements (they are disjoint), the intersection of A and A′ is the empty set.
Answer: A∩A′=Φ
(iv) U′∩A=…
- Explanation: U′ is the complement of the universal set U, which is the empty set Φ, because there are no elements outside the universal set. The intersection of the empty set with any set A is always the empty set.
Answer: U′∩A=Φ
Exercise 1.6 (Chapter 1 Sets)
1. If X and Y are two sets such that n(X) = 17, n(Y) = 23, and n(X ∪ Y) = 38, find n(X ∩ Y).
Solution:
We are given the following information:
- n(X)=17,
- n(Y)=23,
- n(X∪Y)=38.
We need to find n(X∩Y), the number of elements in the intersection of X and Y.
Formula for Union of Two Sets:
The formula for the number of elements in the union of two sets X and Y is:
n(X∪Y)=n(X)+n(Y)−n(X∩Y)
Substitute the Given Values:
38=17+23−n(X∩Y)
Simplify the Equation:
38=40−n(X∩Y)
n(X∩Y)=40−38=2
Answer:
The number of elements in the intersection of X and Y is: n(X∩Y)=2
2. If X and Y are two sets such that X ∪Y has 18 elements, X has 8 elements and Y has 15 elements; how many elements does X ∩ Y have?
Solution:
We are given the following information:
- n(X∪Y)=18,
- n(X)=8,
- n(Y)=15.
We are asked to find n(X∩Y), the number of elements in the intersection of X and Y.
The formula for the Union of Two Sets:
The formula for the number of elements in the union of two sets X and Y is:
n(X∪Y)=n(X)+n(Y)−n(X∩Y)
Substitute the Given Values:
18=8+15−n(X∩Y)
18=23−n(X∩Y)
n(X∩Y)=23−18=5
Answer:
The number of elements in the intersection of X and Y is: n(X∩Y)=5
3. In a group of 400 people, 250 can speak Hindi and 200 can speak English. How many people can speak both Hindi and English?
Solution:
We are given the following information:
- Total number of people = 400,
- Number of people who can speak Hindi = 250,
- Number of people who can speak English = 200.
We are asked to find how many people can speak both Hindi and English, i.e., the number of people in the intersection of the two sets (Hindi speakers and English speakers).
Formula for the Union of Two Sets:
The formula for the number of people in the union of two sets AAA (Hindi speakers) and BBB (English speakers) is:
n(A∪B)=n(A)+n(B)−n(A∩B)
Where:
- n(A∪B) is the total number of people who can speak either Hindi or English or both.
- n(A) is the number of people who can speak Hindi.
- n(B) is the number of people who can speak English.
- n(A∩B) is the number of people who can speak both Hindi and English.
Substitute the Given Values:
We know:
- n(A∪B)=400 (since there are 400 people in total),
- n(A)= (Hindi speakers),
- n(B)=200 (English speakers).
Substitute these values into the formula:
400=250+200−n(A∩B)
Simplify the Equation:
400=450−n(A∩B)
Now, solve for n(A∩B):
n(A∩B)=450−400=50
Answer:
The number of people who can speak both Hindi and English is: n(A∩B)=50
4. If S and T are two sets such that S has 21 elements, T has 32 elements, and S ∩ T has 11 elements, how many elements does S ∪ T have?
Solution:
We are given the following information:
- n(S)=21 (The number of elements in set SSS),
- n(T)=32 (The number of elements in set TTT),
- n(S∩T)=11 (The number of elements in the intersection of sets S and T).
We are asked to find n(S∪T), the number of elements in the union of sets S and T.
The formula for the Union of Two Sets:
n(S∪T)=n(S)+n(T)−n(S∩T)
Substitute the Given Values:
n(S∪T)=21+32−11
n(S∪T)=53−11=42
Answer:
The number of elements in the union of sets S and T is: n(S∪T)=42
5. If X and Y are two sets such that X has 40 elements, X ∪Y has 60 elements and X ∩Y has 10 elements, how many elements does Y have?
Solution:
We are given the following information:
- n(X)=40 (The number of elements in set X),
- n(X∪Y)=60 (The number of elements in the union of sets X and Y),
- n(X∩Y)=10 (The number of elements in the intersection of sets X and Y).
We are asked to find n(Y), the number of elements in set Y.
The formula for the Union of Two Sets:
n(X∪Y)=n(X)+n(Y)−n(X∩Y)
Substitute the Given Values:
60=40+n(Y)−10
60=30+n(Y)
n(Y)=60−30=30
Answer:
The number of elements in set Y is: n(Y)=30
6. In a group of 70 people, 37 like coffee, 52 like tea, and each person likes at least one of the two drinks. How many people like both coffee and tea?
Solution:
We are given the following information:
- Total number of people = 70,
- Number of people who like coffee = 37,
- Number of people who like tea = 52,
- Each person likes at least one of the two drinks (coffee or tea).
We need to find how many people like both coffee and tea, i.e., the number of people in the intersection of the two sets (coffee drinkers and tea drinkers).
Formula for the Union of Two Sets:
The formula for the number of people in the union of two sets A (coffee drinkers) and B (tea drinkers) is:
n(A∪B)=n(A)+n(B)−n(A∩B))
Where:
- n(A∪B) is the total number of people who like either coffee, tea, or both (which is 70, because each person likes at least one drink),
- n(A)=37 (number of people who like coffee),
- n(B)=52 (number of people who like tea),
- n(A∩B) is the number of people who like both coffee and tea.
Substitute the Given Values:
70=37+52−n(A∩B)
70=89−n(A∩B)
n(A∩B)=89−70=19
Answer:
The number of people who like both coffee and tea is: n(A∩B)=19
7. In a group of 65 people, 40 like cricket, 10 like both cricket and tennis. How many like tennis only and not cricket? How many like tennis?
Solution:
We are given:
- Total number of people = 65,
- 40 people like cricket,
- 10 people like both cricket and tennis.
We need to find:
- The number of people who like tennis only.
- The total number of people who like tennis.
Step 1: Find the Total Number of People Who Like Tennis
Using the formula for the union of two sets:
n(C∪T)=n(C)+n(T)−n(C∩T)
Substitute the given values:
65=40+n(T)−10
Solve for n(T):
n(T)=65−30=35
Step 2: Find the Number of People Who Like Tennis Only
The number of people who like tennis only is:
n(T only)=n(T)−n(C∩T)=35−10=25
Answer: Tennis only: 25 people and Total tennis lovers: 35 people.
8. In a committee, 50 people speak French, 20 speak Spanish and 10 speak both Spanish and French. How many speak at least one of these two languages?
Solution:
We are given the following information:
- 50 people speak French,
- 20 people speak Spanish,
- 10 people speak both Spanish and French.
We need to find how many people speak at least one of these two languages (French or Spanish).
Using the Principle of Inclusion-Exclusion:
The formula for the number of people who speak at least one of the two languages is:
n(F∪S)=n(F)+n(S)−n(F∩S)
Where:
- n(F)=50 (people who speak French),
- n(S)=20 (people who speak Spanish),
- n(F∩S)=10 (people who speak both languages).
Substitute the Values:
n(F∪S)=50+20−10=60
Answer:
The number of people who speak at least one of the two languages (French or Spanish) is: 60
Miscellaneous Exercise (Chapter 1 Sets)
1. Decide, among the following sets, which sets are subsets of one and another:
A= {x: x ∈ R and x satisfy x2 – 8x + 12 = 0},
B = {2, 4, 6},
C = {2, 4, 6, 8…},
D = {6}.
Solution:
According to the question,
We have,
A = {x: x ∈ R and x satisfies x2 – 8x + 12 =0}
2 and 6 are the only solutions of x2 – 8x + 12 = 0.
Hence, A = {2, 6}
B = {2, 4, 6}, C = {2, 4, 6, 8 …}, D = {6}
Now, let’s compare the sets to check for subset relationships.
(i) A⊆B
(ii) B⊈AB
(iii) A⊆C
(iv) C⊈A
(v) A⊈D
(vi) D⊆A
2. In each of the following, determine whether the statement is true or false. If it is true, prove it. If it is false, give an example.
(i) If x ∈ A and A ∈ B, then x ∈ B
(ii) If A ⊂ B and B ∈ C, then A ∈ C
(iii) If A ⊂ B and B ⊂ C, then A ⊂ C
(iv) If A ⊄ B and B ⊄ C, then A ⊄ C
(v) If x ∈ A and A ⊄ B, then x ∈ B
(vi) If A ⊂ B and x ∉ B, then x ∉ A
Solution:
(i) False
According to the question,
A = {1, 2} and B = {1, {1, 2}, {3}}
Now, we have,
2 ∈ {1, 2} and {1, 2} ∈ {1, {1, 2}, {3}}
Hence, we get,
A ∈ B
We also know,
{2} ∉ {1, {1, 2}, {3}}
(ii) False
According to the question
Let us assume that,
A {2}
B = {0, 2}
And, C = {1, {0, 2}, 3}
From the question,
A ⊂ B
Hence,
B ∈ C
But, we know,
A ∉ C
(iii) True
According to the question
A ⊂ B and B ⊂ C
Let us assume that,
x ∈ A
Then, we have,
x ∈ B
And,
x ∈ C
Therefore,
A ⊂ C
(iv) False
According to the question
A ⊄ B
Also,
B ⊄ C
Let us assume that,
A = {1, 2}
B = {0, 6, 8}
And,
C = {0, 1, 2, 6, 9}
∴ A ⊂ C
(v) False
According to the question,
x ∈ A
Also,
A ⊄ B
Let us assume that,
A = {3, 5, 7}
Also,
B = {3, 4, 6}
We know that,
A ⊄ B
∴ 5 ∉ B
(vi) True
According to the question,
A ⊂ B
Also,
x ∉ B
Let us assume that,
x ∈ A,
We have,
x ∈ B,
From the question,
We have, x ∉ B
∴ x ∉ A
3. Let A, B and C be the sets such that A ∪ B = A ∪ C and A ∩ B = A ∩ C. show that B = C.
Solution:
According to the question,
A ∪ B = A ∪ C
And,
A ∩ B = A ∩ C
To show,
B = C
Let us assume,
x ∈ B
So,
x ∈ A ∪ B
x ∈ A ∪ C
Hence,
x ∈ A or x ∈ C
When x ∈ A, then,
x ∈ B
∴ x ∈ A ∩ B
As, A ∩ B = A ∩ C
So, x ∈ A ∩ C
∴ x ∈ A or x ∈ C
x ∈ C
∴ B ⊂ C
Similarly, it can be shown that C ⊂ B
Hence, B = C
4. Show that the following four conditions are equivalent:
(i) A ⊂ B (ii) A – B = Φ
(iii) A ∪ B = B (iv) A ∩ B = A
Solution:
(i) A⊂B ⟹ A−B=∅:
- Proof:
- If A⊂B, then every element of A is also in B.
- Therefore, there are no elements in A that are not in B, which means A−B=∅.
- Hence, A⊂B ⟹ A−B=∅, implies A – B =∅.
(ii) A−B=∅ ⟹ A⊂BA – B:
- Proof:
- If A−B=∅A – B =∅, this means there are no elements in A that are not in B.
- Therefore, every element of A must be in B, which means A⊂B.
- Hence, A−B=∅ ⟹ A⊂B.
(iii) A⊂B ⟹ A∪B=B:
- Proof:
- If A⊂B, then every element of A is also in B.
- Therefore, the union A∪B will be equal to B, because adding elements of A to B does not introduce anything new.
- Hence, A⊂B ⟹ A∪B=B.
(iv) A∪B=B ⟹ A⊂B:
- Proof:
- If A∪B=B, then every element in A must also be in B, because the union of A and B does not introduce any elements outside B.
- Hence, A⊂B.
- Therefore, A∪B=B ⟹ A⊂B.
(v) A⊂B ⟹ A∩B=A:
- Proof:
- If A⊂B, then every element of A is also in B.
- The intersection A∩B consists of all elements that are in both A and B.
- Since A⊂B, all elements of A are in B, so A∩B=A.
- Hence, A⊂B ⟹ A∩B=A.
(vi) A∩B=A ⟹ A⊂B:
- Proof:
- If A∩B=A, then every element of A must also be in B, because the intersection of A and B contains all elements of A.
- Hence, A⊂B.
- Therefore, A∩B=A ⟹ A⊂B.
5. Show that if A ⊂ B, then C – B ⊂ C – A.
Solution:
To show,
C – B ⊂ C – A
According to the question,
Let us assume that x is any element such that X ∈ C – B
∴ x ∈ C and x ∉ B
Since, A ⊂ B, we have,
∴ x ∈ C and x ∉ A
So, x ∈ C – A
∴ C – B ⊂ C – A
Hence, Proved.
6. Assume that P (A) = P (B). Show that A = B
Solution:
To show,
A = B
According to the question,
P (A) = P (B)
Let x be any element of set A,
x ∈ A
Since, P (A) is the power set of set A, it has all the subsets of set A.
A ∈ P (A) = P (B)
Let C be an element of set B
For any C ∈ P (B),
We have, x ∈ C
C ⊂ B
∴ x ∈ B
∴ A ⊂ B
Similarly, we have:
B ⊂ A
SO, we get,
If A ⊂ B and B ⊂ A
∴ A = B
7. Is it true that for any sets A and B, P (A) ∪ P (B) = P (A ∪ B)? Justify your answer.
Solution:
The statement P(A)∪P(B)=P(A∪B) is false.
Reason:
- P(A)∪P(B) contains all subsets of A and B, but not necessarily all subsets of A∪B.
- P(A∪B) contains all subsets of A∪B, including those that combine elements from both A and B.
Counterexample:
Let A={1,2} and B={2,3}. Then:
- P(A)∪P(B) does not include {1,3, but P(A∪B) does.
Hence, P(A)∪P(B)≠P(A∪B).
8. Show that for any sets A and B,
A = (A ∩ B) ∪ (A – B) and A ∪ (B – A) = (A ∪ B)
Solution:
To Prove: A = (A ∩ B) ∪ (A – B)
Proof: Let x ∈ A
To show,
X ∈ (A ∩ B) ∪ (A – B)
In Case I,
X ∈ (A ∩ B)
⇒ X ∈ (A ∩ B) ⊂ (A ∪ B) ∪ (A – B)
In Case II,
X ∉A ∩ B
⇒ X ∉ B or X ∉ A
⇒ X ∉ B (X ∉ A)
⇒ X ∉ A – B ⊂ (A ∪ B) ∪ (A – B)
∴A ⊂ (A ∩ B) ∪ (A – B) (i)
It can be concluded that, A ∩ B ⊂ A and (A – B) ⊂ A
Thus, (A ∩ B) ∪ (A – B) ⊂ A (ii)
Equating (i) and (ii),
A = (A ∩ B) ∪ (A – B)
We also have to show,
A ∪ (B – A) ⊂ A ∪ B
Let us assume,
X ∈ A ∪ (B – A)
X ∈ A or X ∈ (B – A)
⇒ X ∈ A or (X ∈ B and X ∉A)
⇒ (X ∈ A or X ∈ B) and (X ∈ A and X ∉A)
⇒ X ∈ (B ∪A)
∴ A ∪ (B – A) ⊂ (A ∪ B) (iii)
According to the question,
To prove: (A ∪ B) ⊂ A ∪ (B – A)
Let y ∈ A∪B
Y ∈ A or y ∈ B
(y ∈ A or y ∈ B) and (X ∈ A and X ∉A)
⇒ y ∈ A or (y ∈ B and y ∉A)
⇒ y ∈ A ∪ (B – A)
Thus, A ∪ B ⊂ A ∪ (B – A) (iv)
∴From equations (iii) and (iv), we get:
A ∪ (B – A) = A ∪ B
9. Using properties of sets, show that:
(i) A ∪ (A ∩ B) = A
(ii) A ∩ (A ∪ B) = A.
Solution:
(i) A∪(A∩B)=A:
Step 1: We need to show that every element of A∪(A∩B) is also in A, and vice versa.
Step 2:
- A∪(A∩B) is the union of two sets: A and A∩B
- By the definition of union, A∪(A∩B) consists of all elements that are either in A or in A∩B.
Step 3:
- If an element xxx is in A∪(A∩B), then xxx is either in A or in A∩B.
- If x∈A∩B, then x∈A by definition of intersection.
- Therefore, in both cases (whether x∈A or x∈A∩B), x∈A.
Thus, A∪(A∩B)⊆A.
Step 4:
- Clearly, A⊆A∪(A∩B), because A is a subset of the union.
Step 5: Since both A⊆A∪(A∩B) and A∪(A∩B)⊆A, we conclude that:
A∪(A∩B)=A
(ii) A∩(A∪B)=A:
Step 1: We need to show that every element of A∩(A∪B) is also in A, and vice versa.
Step 2:
- A∩(A∪B) is the intersection of A and A∪B.
- By the definition of intersection, A∩(A∪B) consists of all elements that are in both A and A∪B.
Step 3:
- Every element of A is automatically in A∪BA \cup BA∪B, because A⊆A∪BA \subseteq A \cup BA⊆A∪B.
- Therefore, every element of A is in both A and A∪B, and hence, in A∩(A∪B).
Thus, A⊆A∩(A∪B).
Step 4:
- Clearly, A∩(A∪B)⊆A, because the intersection of A with any set cannot have elements outside A.
Step 5: Since both A⊆A∩(A∪B)) and A∩(A∪B)⊆A, we conclude that:
A∩(A∪B)=A
10. Show that A ∩ B = A ∩ C need not imply B = C.
Solution:
Let us assume,
A = {0, 1}
B = {0, 2, 3}
And, C = {0, 4, 5}
According to the question,
A ∩ B = {0}
And,
A ∩ C = {0}
∴ A ∩ B = A ∩ C = {0}
But,
2 ∈ B and 2 ∉ C
Therefore, B ≠ C
11. Let A and B be sets. If A ∩ X = B ∩ X = ϕ and A ∪ X = B ∪ X for some set X, show that A = B.
(Hints A = A ∩ (A ∪ X) , B = B ∩ (B ∪ X) and use Distributive law)
Solution:
We will use the distributive law and the given conditions to prove that A=BA = BA=B.
Step 1: Expression for A and B using distributive property
First, recall the distributive property of set operations:
A=A∩(A∪X)A, B=B∩(B∪X)B
These two equations follow from the fact that a set is always equal to its intersection with the union of itself and another set.
Step 2: Use the given condition A∪X=B∪X
We are given that A∪X=B∪X. So, we can substitute this into the above expressions:
A=A∩(A∪X)=A∩(B∪X)
B=B∩(B∪X)=B∩(A∪X)
Now, we have:
- A=A∩(B∪X)
- B=B∩(A∪X)
Step 3: Simplify using A∩X=B∩X=∅
We are given that A∩X=∅ and B∩X=∅. This means that neither A nor B contains any elements of X.
Using this in the expressions for A and B:
- A=A∩(B∪X) simplifies to A=A∩B, because A∩X=∅ (there are no elements of A in X).
- Similarly, B=B∩(A∪X) simplifies to B=B∩A, because B∩X=∅ (there are no elements of B in X).
Step 4: Conclude that A=B
Now, we have:
- A=A∩B
- B=B∩A
Since A=A∩B and B=B∩A, it follows that A=B.
12. Find sets A, B and C such that A ∩ B, B ∩ C and A ∩ C are non-empty sets and A∩B∩C = Φ.
Solution:
Let us assume, A {0, 1}
B = {1, 2}
And, C = {2, 0}
According to the question,
A ∩ B = {1}
B ∩ C = {2}
And,
A ∩ C = {0}
∴ A ∩ B, B ∩ C and A ∩ C are not empty sets
Hence, we get,
A ∩ B ∩ C = Φ
13. In a survey of 600 students in a school, 150 students were found to be taking tea and 225 taking coffee, 100 were taking both tea and coffee. Find how many students were taking neither tea nor coffee.
Solution:
Let us assume that,
U = the set of all students who took part in the survey
T = the set of students taking tea
C = the set of the students taking coffee
Total number of students in a school, n (U) = 600
Number of students taking tea, n (T) = 150
Number of students taking coffee, n (C) = 225
Also, n (T ∩ C) = 100
Now, we have to find that number of students taking neither coffee nor tea i.e. n (T ∩ C’)
∴ According to the question,
n ( T ∩ C’ )= n( T ∩ C )’
= n (U) – n (T ∩ C)
= n (U) – [n (T) + n(C) – n (T ∩ C)]
= 600 – [150 + 225 – 100]
= 600 – 275
= 325
∴ Number of students taking neither coffee nor tea = 325 students.
14. In a group of students, 100 students know Hindi, 50 know English and 25 know both. Each of the students knows either Hindi or English. How many students are there in the group?
Solution:
Given:
- Number of students who know Hindi = 100
- Number of students who know English = 50
- Number of students who know both Hindi and English = 25
- Each student knows either Hindi or English.
We can use the principle of inclusion-exclusion to solve this.
Let:
- H be the set of students who know Hindi. E be the set of students who know English.
The number of students who know either Hindi or English (or both) is: ∣H∪E∣=∣H∣+∣E∣−∣H∩E∣
Where:
- ∣H∣=100 (students who know Hindi)
- ∣E∣=50 (students who know English)
- ∣H∩E∣=25 (students who know both Hindi and English)
Now, calculate the total number of students who know either Hindi or English:
∣H∪E∣=(100)+(50)−(25)=125
Answer: The total number of students in the group is 125.
15. In a survey of 60 people, it was found that 25 people read newspaper H, 26 read newspaper T, 26 read newspaper I, 9 read both H and I, 11 read both H and T, 8 read both T and I, 3 read all three newspapers. Find:
(i) The number of people who read at least one of the newspapers.
(ii) The number of people who read exactly one newspaper.
Solution:
Given:
- Total number of people = 60
- Number of people who read newspaper H = 25
- Number of people who read newspaper T = 26
- Number of people who read newspaper I = 26
- Number of people who read both H and I = 9
- Number of people who read both H and T = 11
- Number of people who read both T and I = 8
- Number of people who read all three newspapers = 3
(i) Number of people who read at least one newspaper (H ∪ T ∪ I):
To find the number of people who read at least one newspaper, we use the inclusion-exclusion principle:
n(H∪T∪I)=n(H)+n(T)+n(I)−n(H∩T)−n(T∩I)−n(H∩I)+n(H∩T∩I)
Substitute the given values:
n(H∪T∪I)=25+26+26−11−8−9+3=52
Therefore, 52 people read at least one newspaper.
(ii) Number of people who read exactly one newspaper:
To find the number of people who read exactly one newspaper, we subtract the people who read two or three newspapers from those who read each newspaper.
- Exactly H = n(H)−n(H∩T)−n(H∩I)+n(H∩T∩I)
n(Exactly H)=25−11−9+3=8
- Exactly T = n(T)−n(T∩H)−n(T∩I)+n(H∩T∩I)
n(Exactly T)=26−11−8+3=10
- Exactly I = n(I)−n(I∩H)−n(I∩T)+n(H∩T∩I)
n(Exactly I)=26−9−8+3=12
Therefore, the number of people who read exactly one newspaper is: n(Exactly one)=8+10+12=30
16. In a survey it was found that 21 people liked product A, 26 liked product B and 29 liked product C. If 14 people liked products A and B, 12 people liked products C and A, 14 people liked products B and C and 8 liked all the three products. Find how many liked product C only.
Solution:
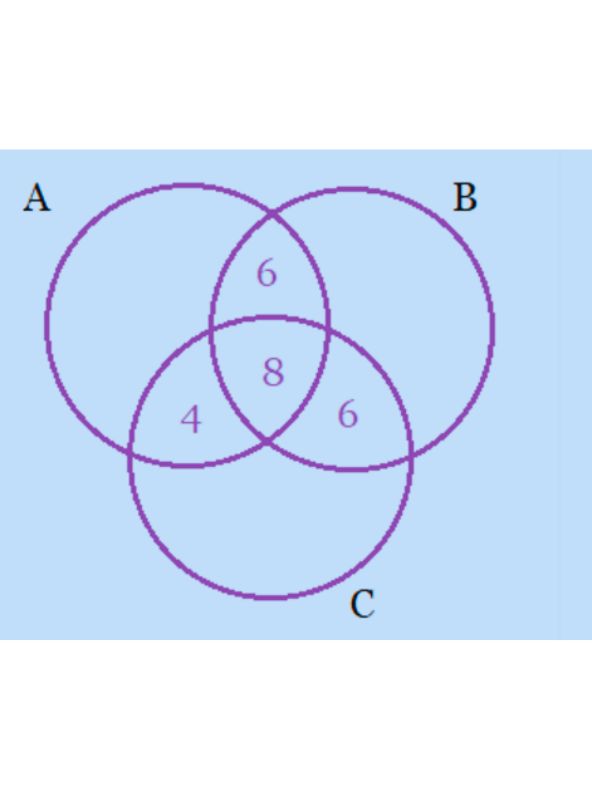
Given:
- 21 people liked product A
- 26 people liked product B
- 29 people liked product C
- 14 people liked both products A and B
- 12 people liked both products A and C
- 14 people liked both products B and C
- 8 people liked all three products (A, B, and C)
We need to find how many people liked only product C.
Using the principle of inclusion-exclusion:
Let’s define the sets: A = people who like product A. B = people who like product B. C = people who like product C
The principle of inclusion-exclusion for three sets is:
n(A∪B∪C)=n(A)+n(B)+n(C)−n(A∩B)−n(B∩C)−n(C∩A)+n(A∩B∩C)
Where:
- n(A)=21
- n(B)=26
- n(C)=29
- n(A∩B)=14
- n(B∩C)=14
- n(C∩A)=12
- n(A∩B∩C)=8
Step 1: Number of people who liked only product C
To find the number of people who liked only product C, we need to subtract those who liked products that are not just C (i.e., those who liked C along with A or B) from the total who liked C.
So, the number of people who liked only C is:
n(Only C)=n(C)−n(C∩A)−n(C∩B)+n(A∩B∩C)
Substitute the given values: n(Only C)=29−12−14+8=11
Hope you find these solutions helpful in understanding the concepts of Class 11 Chapter 1 Maths. Click here for solutions to Class 12 Maths Chapter.


